GCF of 6 and 12
GCF of 6 and 12
The simplest way to find the greatest common factor (GCF) of 6 and 12 is by listing their factors. The factors of 6 are 1, 2, 3, and 6, while the factors of 12 are 1, 2, 3, 4, 6, and 12. Examining these lists, the common factors are 1, 2, 3, and 6. The largest of these common factors is 6, making it the GCF of 6 and 12. This method of listing factors is straightforward and efficient for smaller numbers, providing a quick solution to identify the highest number that divides both integers without a remainder.
GCF of 6 and 12
GCF of 6 and 12 is 6.
GCF of 6 and 12 by Prime Factorization Method.
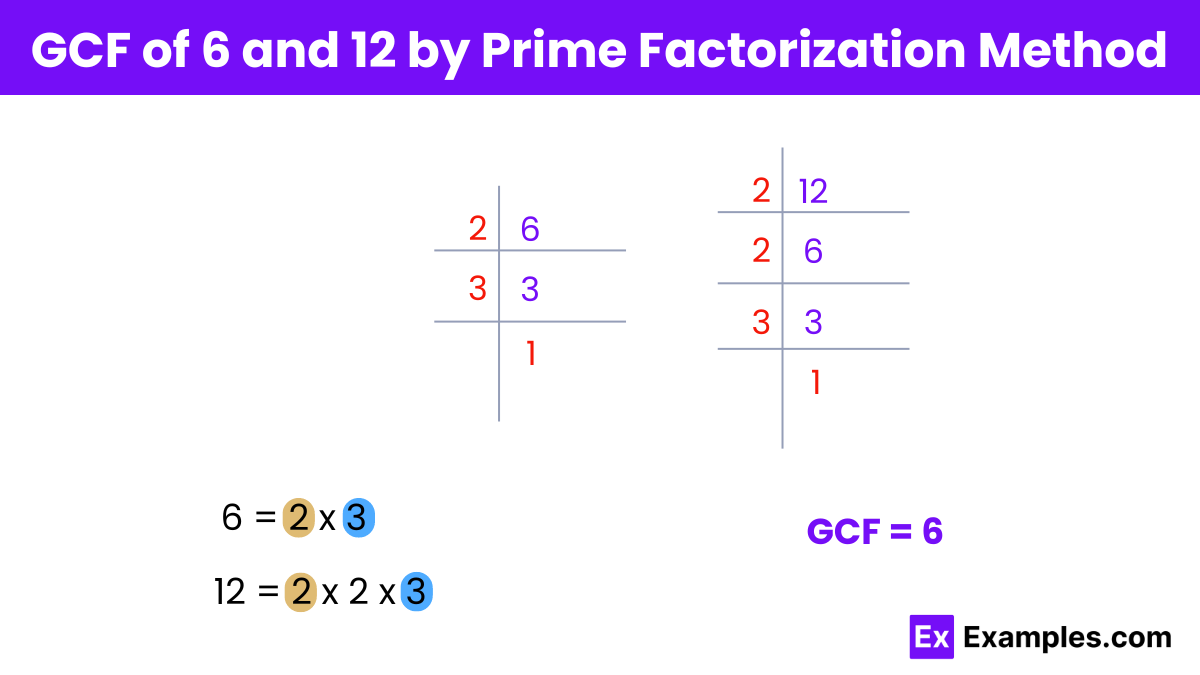
To find the greatest common factor (GCF) of 6 and 12 using the prime factorization method:
Step 1: Prime factorize both numbers:
For 6: 6 = 2 × 3
For 12: 12 = 2² × 3
Step 2: Identify the common prime factors and their lowest powers:
- The common prime factors between 6 and 12 are 2 and 3. The lowest powers are 212^121 and 313^131.
Step 3: Multiply the common prime factors with their lowest powers to determine the GCF:
GCF = 2¹ × 3¹= 2 × 3 = 6
Therefore, the greatest common factor (GCF) of 6 and 12 by the prime factorization method is 6.
GCF of 6 and 12 by Long Division Method.
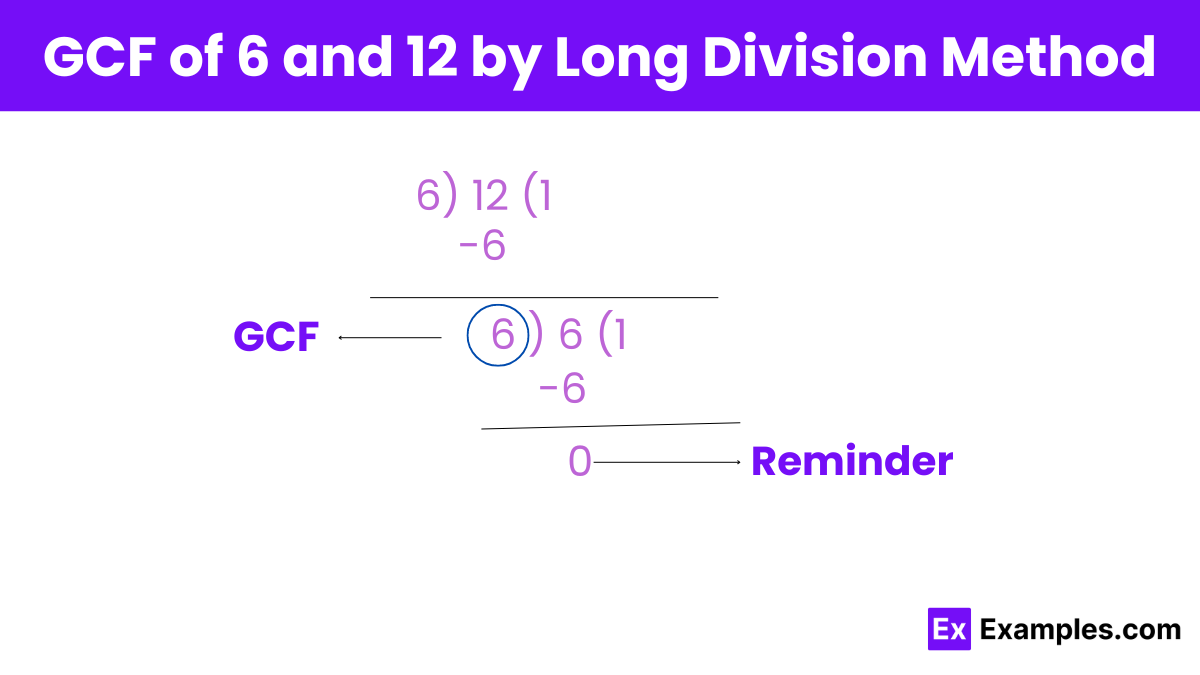
To find the greatest common factor (GCF) of 6 and 12 using the long division method:
Step 1: Start by dividing the larger number (12) by the smaller number (6).
12 ÷ 6 = 2 with a remainder of 0.
Since there is no remainder, the division process stops here.
Step 2: The divisors at this step where the remainder becomes zero is the greatest common factor (GCF).
GCF = 6.
Therefore, the greatest common factor (GCF) of 6 and 12 by the long division method is 6.
GCF of 6 and 12 by Listing Common Factors.
To find the greatest common factor (GCF) of 6 and 12 by listing common factors:
Step 1: List the factors of each number.
Factors of 6: 1, 2, 3, 6
Factors of 12: 1, 2, 3, 4, 6, 12
Step 2: Identify the common factors.
- Common factors: 1, 2, 3, 6
Step 3: Determine the greatest common factor.
The highest number in the list of common factors is 6.
Can you use the Euclidean algorithm to find the GCF of 6 and 12?
Yes, the Euclidean algorithm involves dividing the larger number by the smaller and then using the remainder to find the GCF.
How does understanding the GCF of 6 and 12 help in real life?
It can be used in situations involving equal distribution or partitioning items into smaller groups.
How does the GCF relate to the least common multiple (LCM) for 6 and 12?
The GCF is used along with the product of the numbers to find the LCM.
What if the numbers change slightly, how would you find the GCF of 6 and 13?
Since 13 is prime and does not share any common factors with 6 other than 1, the GCF would be 1.
What is the importance of the GCF in algebra?
In algebra, the GCF is crucial for simplifying polynomial expressions.
What are the common mistakes when finding the GCF of 6 and 12?
Overlooking smaller factors or confusing the GCF with the LCM.
Share :
