Prime Factorization

Prime factorization, the process of breaking down a number into the set of prime numbers that multiply together to result in the original number, is a cornerstone of number theory. Through engaging examples and clear, concise explanations, this guide aims to demystify the process, showcasing its practicality and importance in various mathematical applications, from solving greatest common divisor (GCD) problems to simplifying fractions. Whether you’re tackling homework problems or exploring mathematical theories, mastering prime factorization is a skill that enhances both academic and real-world mathematical proficiency.

What is Prime Factorization?

Prime factorization is the method of expressing a number as the product of its prime factors. This fundamental concept in mathematics involves breaking down a composite number into a combination of prime numbers that, when multiplied together, give back the original number. For example, the prime factorization of 12 is 2 x 2 x 3, indicating that when the prime numbers 2 and 3 are multiplied together in this manner, the result is 12. Understanding prime factorization is crucial for various mathematical operations, including simplifying fractions and finding the least common multiple (LCM) or greatest common divisor (GCD) of two numbers. It’s a key skill that enhances one’s ability to work with numbers and solve a wide range of mathematical problems.

Prime Factorization Solved Examples

Here are several examples of prime factorization, demonstrating how to break down composite numbers into their prime factors:

Example 1: Prime Factorization of 18

• Number: 18
• Factors: $2\times 3\times 3$ or 2×3²
• Explanation: 18 can be divided by 2 to get 9, which can then be divided by 3 twice, resulting in the prime factors 2 and 3.

Example 2: Prime Factorization of 30

• Number: 30
• Factors: $2\times 3\times 5$
• Explanation: 30 is divisible by 2 to get 15, which can then be divided by 3 to get 5; all divisors 2, 3, and 5 are prime.

Example 3: Prime Factorization of 100

• Number: 100
• Factors: 2×2×5×5 or 2²×5⁵
• Explanation: 100 is divisible by 2 to get 50, which is again divisible by 2 to get 25, which can then be divided by 5 twice, yielding prime factors 2 and 5.

Example 4: Prime Factorization of 60

• Number: 60
• Factors: 2×2×5×5 or 22×3×5
• Explanation: Starting with 60, it is divisible by 2 twice to get 15, which is then divisible by 3 and 5, revealing the prime numbers 2, 3, and 5.

Example 5: Prime Factorization of 84

• Number: 84
• Factors:2×2×3×7 or 2²×3×7
• Explanation: 84 can be divided by 2 to get 42, which is again divisible by 2 to get 21, and then by 3 to get 7, showing that 84’s prime factors are 2, 3, and 7.

Prime Factorization of a Number

Numbers	Prime Factorization
90	2×32×5
100	22×52
84	22×3×7
96	25×3
108	22×33
64	26
75	3×52
80	24×5
125	53
99	32×11
120	23×3×5

Methods of Prime Factorization

There are various methods for the prime factorization of a number. The most common methods that are used for prime factorization are given below:

• Prime factorization by factor tree method
• Prime factorization by division method

Prime Factorization by Factor Tree Method

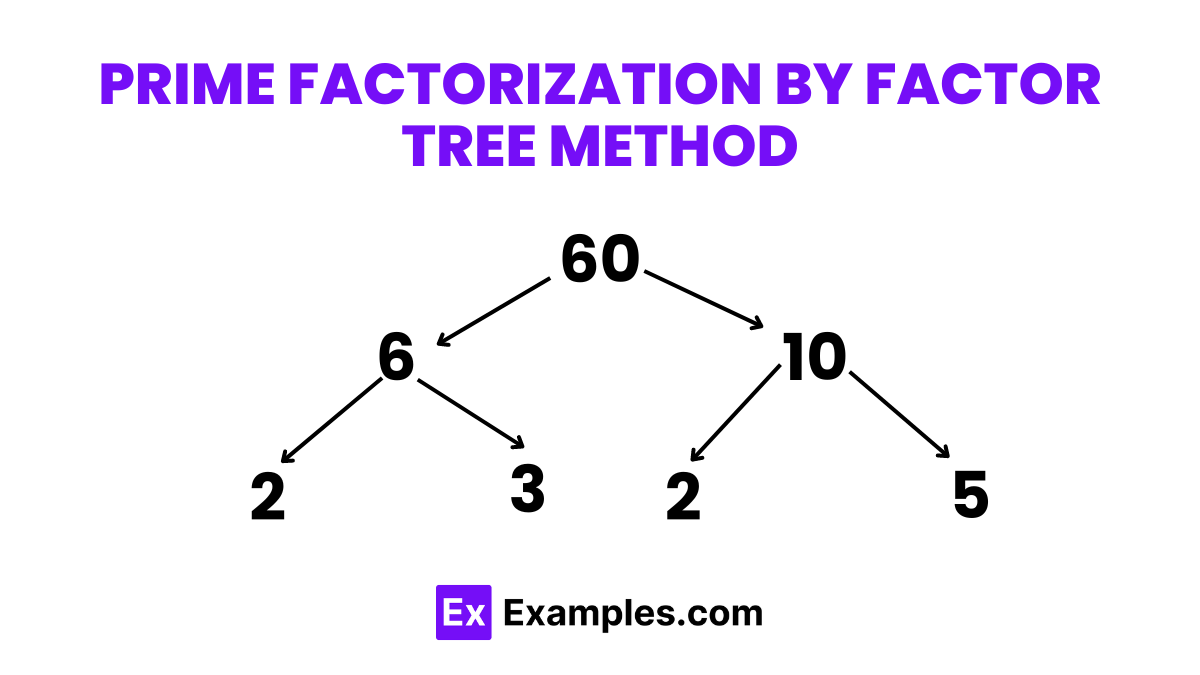
The factor tree method involves breaking down a number into its prime factors by creating a tree diagram. Each branch of the tree splits the number into factors, continuing until all branches end in prime numbers.

Example: Factorize 60 using the factor tree method.

Solution Steps:

1. 1. Start with 60. Split it into any two factors. Let’s use 6 and 10.
   2. Break down 6 into 2 and 3, both prime numbers, so these branches end here.
   3. Break down 10 into 2 and 5, also prime numbers.
   4. Result: The prime factorization of 60 is 2 × 2 × 3 × 5 or 2² × 3 × 5

Prime Factorization by Division Method

The division method for prime factorization involves dividing the number by the smallest possible prime number (2, 3, 5, etc.) until the result is 1. At each step, the divisor that results in a whole number is a prime factor.

Example: Factorize 60 using the division method.

Solution Steps:

1. Start with 60. Divide by the smallest prime number, 2.
   • $60÷2=30$. So, 2 is a prime factor.
2. Continue with 30. It’s also divisible by 2.
   • $30÷2=15$. 2 is a prime factor again.
3. Now, use 15. It’s not divisible by 2, so try the next prime number, 3.
   • $15÷3=5$. So, 3 is a prime factor.
4. Finally, divide by 5.
   • $5÷5=1$. 5 is the last prime factor.
5. Result: The prime factorization of 60 is 2 × 2 × 3 × 5 or 2² × 3 × 5.

These methods offer systematic ways to break down a number into its prime components, each providing a clear pathway through either visual representation or sequential division to arrive at the prime factorization of a number.

Applications of Prime Factorization

Prime factorization, the process of breaking down a number into its prime number components, serves as a cornerstone in mathematics with broad applications. It is crucial for simplifying fractions, finding the greatest common divisors (GCD), least common multiples (LCM), and solving Diophantine equations.

Example: Simplifying the fraction 8/12​ involves prime factorizing the numerator (8 = 2 x 2 x 2) and the denominator (12 = 2 x 2 x 3), leading to its simplest form 2/3 by canceling common factors.

HCF and LCM Using Prime Factorization

Finding the Highest Common Factor (HCF)

The HCF or GCD of two numbers is the highest number that divides both of them without leaving a remainder.

Steps with Example:

1. Choose Numbers: Consider 30 and 45.
2. Prime Factorize: 30 = 2 x 3 x 5; 45 = 3 x 3 x 5.
3. Identify Common Factors: Common prime factors are 3 and 5.
4. Multiply Common Factors: HCF = 3 x 5 = 15.

Finding the Least Common Multiple (LCM)

The LCM of two numbers is the smallest number that is a multiple of both.

Steps with Example:

1. Choose Numbers: Consider 8 and 12.
2. Prime Factorize: 8 = 2 x 2 x 2; 12 = 2 x 2 x 3.
3. Combine Prime Factors: Use the highest power of all prime numbers found in both factorizations (2 x 2 x 2 x 3).
4. Calculate LCM: LCM = 2 x 2 x 2 x 3 = 24.

These methods of using prime factorization to find HCF and LCM showcase its practical utility in solving problems that require understanding the fundamental structure of numbers.

Frequently Asked Questions on Prime Factorization

Why Is Prime Factorization Important?

It’s crucial for various mathematical applications, including simplifying fractions, finding the greatest common divisors (GCD), least common multiples (LCM), and solving problems in number theory.

Can Every Number Be Prime Factorized?

Every composite number can be prime factorized. However, prime numbers and the number 1 are exceptions; prime numbers are their own prime factors, and 1 is not considered because it does not meet the definition of a prime number.

How Do You Find the Prime Factorization of a Number?

To find the prime factorization of a number, divide the number by the smallest prime number (2) and continue dividing by prime numbers (3, 5, 7, etc.) until the quotient is a prime number.

What Is the Difference Between Prime Numbers and Prime Factors?

Prime numbers are natural numbers greater than 1 that have no divisors other than 1 and themselves. Prime factors are prime numbers that multiply together to give a composite number.

Is 1 a Prime Factor?

No, 1 is not considered a prime factor because it does not meet the definition of a prime number, which must have exactly two distinct positive divisors.

Can a Number Have More Than One Set of Prime Factors?

No, the Fundamental Theorem of Arithmetic states that every integer greater than 1 either is prime itself or can be uniquely represented as a product of prime numbers, up to the order of the factors.

How Does Prime Factorization Simplify Fractions?

Prime factorization helps identify common factors in the numerator and denominator of a fraction, allowing them to be cancelled out to simplify the fraction to its lowest terms.

What Role Does Prime Factorization Play in Cryptography?

In cryptography, prime factorization is used in algorithms for public key encryption, where large prime numbers and their products are fundamental to the security of encrypted data.

Are There Efficient Algorithms for Prime Factorization?

While there are algorithms that can perform prime factorization more efficiently than trial division, such as the Sieve of Eratosthenes for finding primes or the Pollard Rho algorithm for factorization, prime factorization of very large numbers remains computationally challenging, which is a basis for the security of many encryption systems.

Prime factorization is a fundamental mathematical process that breaks down composite numbers into their prime components. It’s essential for simplifying fractions, calculating GCD and LCM, and has significant applications in number theory and cryptography. Understanding prime factorization enriches one’s mathematical skills, offering a deeper insight into the structure of numbers and their properties, and highlighting its indispensable role in both academic and practical mathematics.