What is the square of 5?
15
20
25
30


Exploring squares from 1 to 30 delves into fundamental principles of mathematics, including algebra and number theory. Squaring each integer illuminates the intricate relationships between rational and irrational numbers, crucial for understanding concepts like square and square roots. This sequence of squares lays the groundwork for exploring quadratic equations and serves as a cornerstone for more advanced mathematical techniques. Furthermore, it provides valuable insights into the least squares method in statistics, facilitating data analysis and modeling in various fields. Understanding these squares enhances numerical literacy and fosters a deeper appreciation for the elegance and utility of mathematical principles.
Download Squares 1 to 30 in PDF
The square of numbers from 1 to 30 refers to the result obtained by multiplying each integer in this range by itself, showcasing a fundamental mathematical operation that plays a crucial role in algebra, number theory, and various applications.
Highest Value: 30² = 900
Lowest Value: 1² = 1
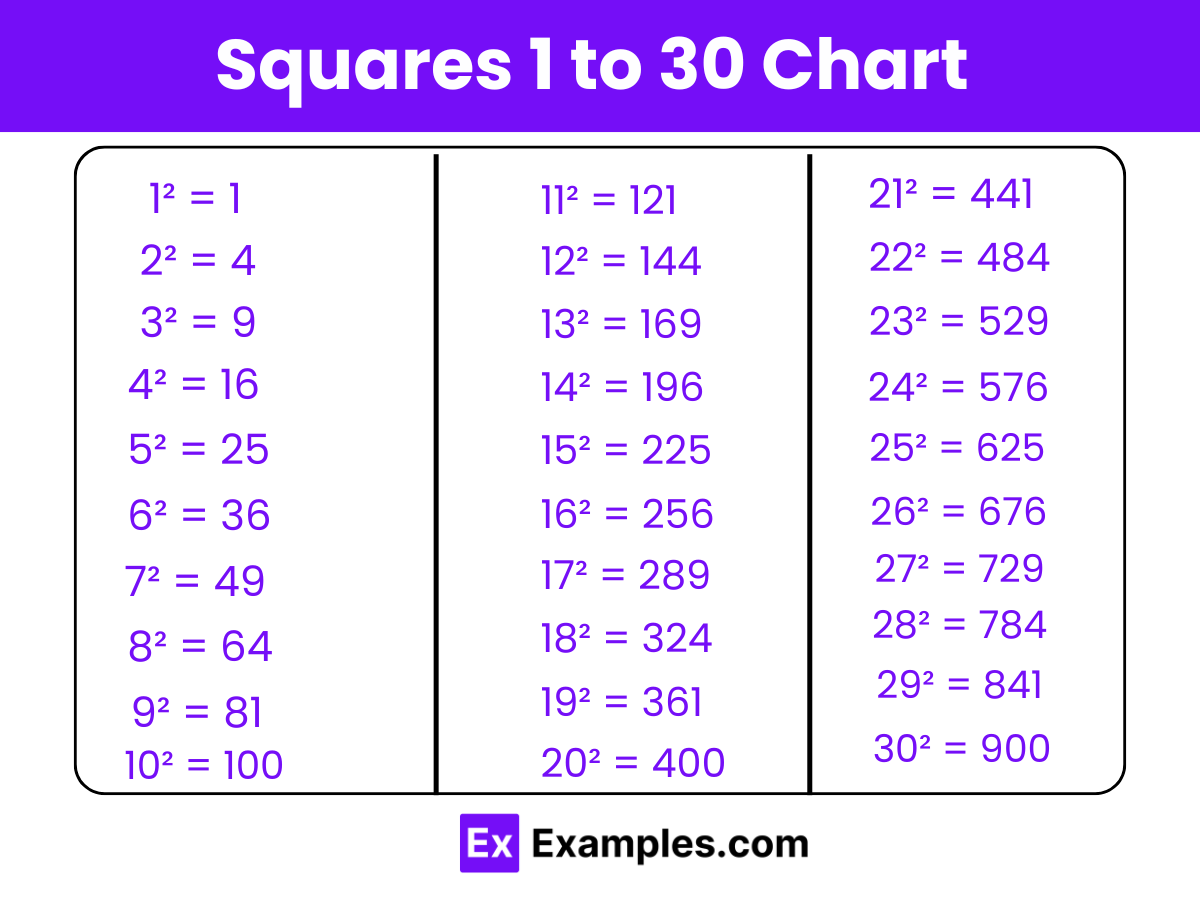
Download Squares 1 to 30 in PDF
| List of All Squares from 1 to 30 | |
| 1² = 1 | 16² = 256 |
| 2² = 4 | 17² = 289 |
| 3² = 9 | 18² = 324 |
| 4² = 16 | 19² = 361 |
| 5² = 25 | 20² = 400 |
| 6² = 36 | 21² = 441 |
| 7² = 49 | 22² = 484 |
| 8² = 64 | 23² = 529 |
| 9² = 81 | 24² = 576 |
| 10² = 100 | 25² = 625 |
| 11² = 121 | 26² = 676 |
| 12² = 144 | 27² = 729 |
| 13² = 169 | 28² = 784 |
| 14² = 196 | 29² = 841 |
| 15² = 225 | 30² = 900 |
Here, squares 1 to 30 can help students to recognize all perfect squares from 1 to 900 and approximate a square root by interpolating between known squares.
| Number | Square |
|---|---|
| 2² | 4 |
| 4² | 16 |
| 6² | 36 |
| 8² | 64 |
| 10² | 100 |
| 12² | 144 |
| 14² | 196 |
| 16² | 256 |
| 18² | 324 |
| 20² | 400 |
| 22² | 484 |
| 24² | 576 |
| 26² | 676 |
| 28² | 784 |
| 30² | 900 |
This table displays the squares of even numbers from 2 to 30, obtained by multiplying each even integer by itself. It highlights the pattern of quadratic growth in even square values, essential in understanding mathematical relationships and applications.
| Number | Square |
|---|---|
| 1² | 1 |
| 3² | 9 |
| 5² | 25 |
| 7² | 49 |
| 9² | 81 |
| 11² | 121 |
| 13² | 169 |
| 15² | 225 |
| 17² | 289 |
| 19² | 361 |
| 21² | 441 |
| 23² | 529 |
| 25² | 625 |
| 27² | 729 |
| 29² | 841 |
This table presents the squares of odd numbers from 1 to 30, showcasing their quadratic growth pattern and fundamental mathematical properties.
To calculate the squares of numbers from 1 to 30, you can follow these steps:
Understand Squaring:
Start from 1 and Go Up to 30:
Use a Calculator for Efficiency:
Record Your Results:
Review the Pattern:
Square numbers exhibit a quadratic growth pattern. When plotted on a graph, they form a parabolic curve. Additionally, certain patterns emerge in the digits of square numbers, providing insights into their properties.
The value of squares 1 to 30 is the list of numbers obtained by multiplying an integer by itself. When we multiply a number by itself we will always get a positive number. For example, the square of 12 is 132 = 169.
You can calculate the squares from 1 to 30 by simply squaring each number individually (e.g., 1212 to 302302) or by using a calculator for efficiency. Additionally, recognizing patterns and employing mental math techniques can expedite the process.
Memorizing the squares of numbers from 1 to 30 can be facilitated through mnemonic devices, visual aids like charts or flashcards, and practice exercises. Breaking down the list into smaller groups can also aid in memorization.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the square of 5?
15
20
25
30
Which of the following is the square of 7?
45
48
49
51
What number squared equals 64?
6
7
8
9
What is the square of 12?
120
124
140
144
Which of the following numbers is not a perfect square?
169
196
224
256
Which of the following is the square of 9?
72
81
85
89
Which of the following numbers is a perfect square?
50
55
60
64
What number squared equals 289?
15
16
17
18
Which of the following is not a perfect square?
25
49
90
121
What number squared equals 81?
7
8
9
10
Before you leave, take our quick quiz to enhance your learning!

