What is the square of 96?
9216
9025
9600
9000

The square of 96 (96²) is calculated by multiplying 96 by itself:
96×96=9216.
So, the square of 96 is 9216.
Geometrically, if you have a square with each side measuring 96 units, the total area enclosed by the square will be 9216 square units.
Understanding the square of 96 is essential in various mathematical contexts, including geometry, algebra, and arithmetic. It finds applications in calculating areas, volumes, distances, and solving mathematical problems.
or
√796=9.798 up to three places of decimal
The square root of 96 (√96) is an irrational number, approximately equal to 9.79898987322.
It represents a number that, when multiplied by itself, results in 96:
√96≈9.7989898732296
Since 96 is not a perfect square, its square root cannot be simplified to a whole number or a simple fraction. Instead, it is a non-repeating, non-terminating decimal.
The square root of 96 finds applications in various fields such as mathematics, physics, engineering, and finance, where precise calculations are required.
Exponential Form: 96^½ or 96^0.5
Radical Form: √96
Since 96 is not a perfect square, its square root cannot be expressed as a fraction of two integers. Additionally, the decimal representation of √96 is non-repeating and non-terminating. Therefore, √96 is classified as an irrational number.
The square root of 96 (√96) is irrational because it cannot be expressed as a simple fraction. Its decimal representation is non-repeating and non-terminating, indicating that it goes on infinitely without a pattern. Since 96 is not a perfect square, its square root cannot be simplified to a rational number. Therefore, √96 is classified as an irrational number in mathematics.
Estimation Method:
Long Division Method:
Newton’s Method:
Using a Calculator or Software:
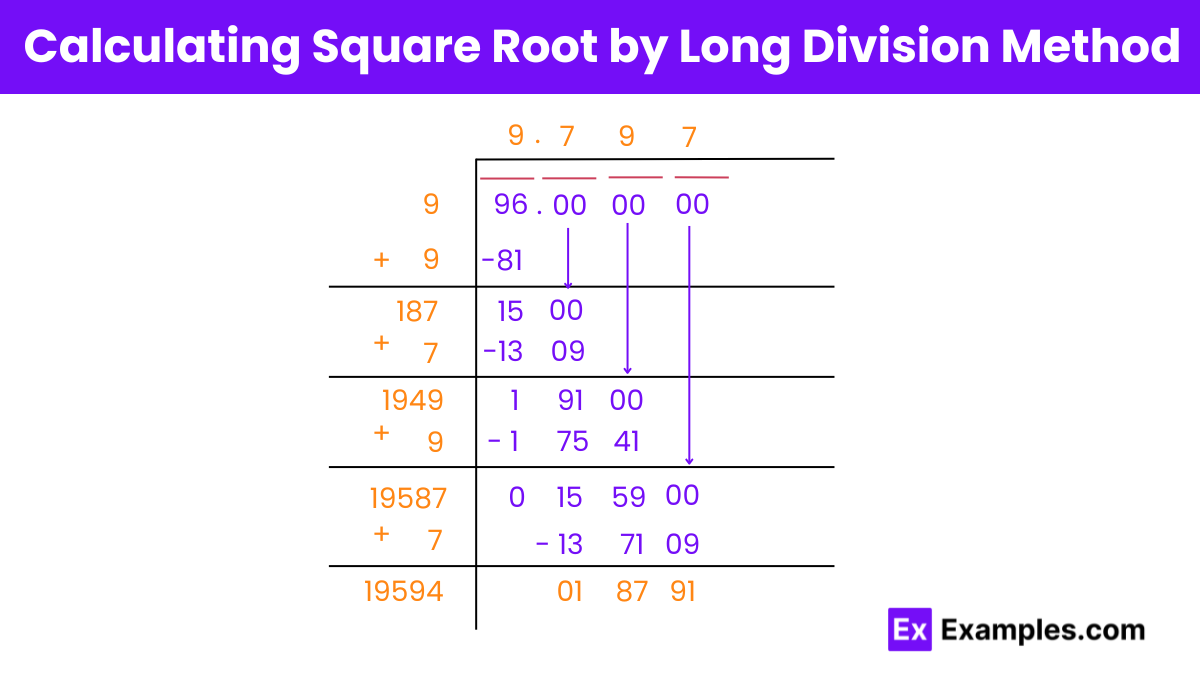
Here’s an alternative presentation of the steps to find the square root of 96 using the long division method:
Digit Pairing: Pair off the digits of the number 96, starting from the right, and place a horizontal bar to indicate pairing.
Initial Estimation: Find a number that, when squared, gives a value less than or equal to 96. In this case, 9 fits as 9×9 = 81. Therefore, the initial quotient and divisor are both 9.
Iteration: Subtract the square of the current divisor from the paired digits to obtain the remainder. Bring down the next pair of digits and continue the process iteratively.
Decimal Placement: Place a decimal point in the quotient and dividend after the whole number part. Add pairs of zeros to the dividend after the decimal point for every pair of digits brought down.
Adjustment: Determine the next digit of the quotient by finding the largest digit that, when appended to the current divisor, gives a product less than or equal to the current remainder. Repeat this process until the desired level of precision is achieved.
Repeat:Continue the steps of bringing down digits, subtracting squares, and finding the next digit of the quotient until all the digits of the square root are determined.
By following these steps iteratively, the square root of 96 can be approximated using the long division method.
A perfect square is a number that can be expressed as the square of an integer. In other words, it is the product of an integer multiplied by itself. For example, 25 is a perfect square because it equals 5×5.
However, 96 cannot be expressed as the product of an integer multiplied by itself. Therefore, it is not a perfect square.
The square root of 96 has applications in fields such as mathematics, physics, engineering, and finance, where precise calculations are required.
Yes, 96 has various mathematical properties and relationships with other numbers, which can be explored in algebraic, geometric, or numerical contexts.
Understanding the square root of 96 and its properties can help in solving practical problems involving measurements, dimensions, areas, volumes, and other quantitative aspects in fields such as construction, engineering, finance, and statistics.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the square of 96?
9216
9025
9600
9000
What is the approximate value of the square root of 96?
9.7
9.8
9.9
10.0
Which number is closest to the square of 96?
9200
9210
9220
9230
If x² = 96, what is the approximate value of x?
9.6
9.7
9.8
9.9
Which statement is true about the square root of 96?
It is a whole number.
It is a rational number.
It is an irrational number.
It is an integer.
What is the result of 96 squared minus 100?
9116
9216
9000
9200
Which of the following is the closest integer to the square root of 96?
9
10
11
12
What is the approximate difference between the square of 96 and the square of 97?
1
2
3
4
If the square root of a number is approximately 9.8, what is the number?
96
98
100
102
Which value represents the closest approximation for the square root of 96 when rounded to one decimal place?
9.7
9.8
9.9
10.0
Before you leave, take our quick quiz to enhance your learning!

