Square Root by Long Division Method

The Long Division method for square roots is a manual technique that provides a precise way to find the square root of any number. It identifies rational roots for perfect squares and square roots approximates irrational roots otherwise, connecting with concepts in algebra and integer operations. This method is significant for both academic learning and practical applications, including in the least squares method of regression analysis. By systematically dividing and estimating, the Long Division method unfolds the intricate relationships between numbers, revealing their mathematical properties.

What is Square Root by Long Division Method?

Square Root of a Perfect Square by Long Division Method

• Pair Digits: Starting from the decimal point, pair the digits of the perfect square moving left for whole numbers and right for decimals.
• Initial Estimate: Find the largest integer whose square is less than or equal to the first pair. This becomes the first digit of the root.
• Subtract and Bring Down: Subtract the square of the first digit from the first pair, then bring down the next pair to form a new number.
• Double the Result: Double the current result to form a new divisor, then append a digit (trial digit) to the divisor and find the largest digit which, when multiplied by the new divisor and itself, is less than or equal to the new number.
• Repeat: Subtract this product from the new number and bring down the next pair of digits. Append the trial digit to the result, and repeat the process until all digit pairs are exhausted.

For Example

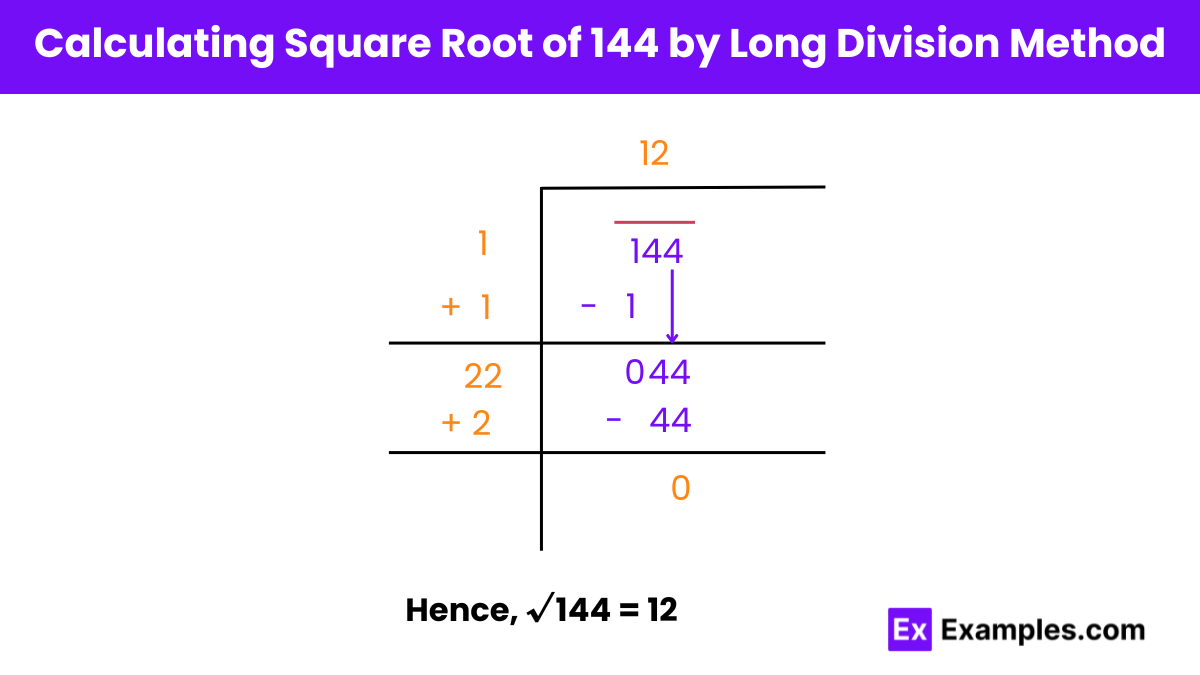
Pair the Digits: Since 144 is a three-digit number, pair the digits from the right: 1|44.

Estimate the Largest Digit: Find the largest integer whose square is less than or equal to 1 (the first pair). This is 1 because 1² = 1. Write this as the first digit of the root.

Current root: 1

Subtract 1² = 1 from 1, which gives 0.

Bring Down the Next Pair: Bring down the next pair 44 to the right of 0 to form 44.

Double the Result: Double the current result, which is 1, to get 2.

New divisor: 2

Find the Largest Digit for the Divisor: Find the largest digit (trial digit) that can be placed in the blank space of the new divisor such that the product of this number with itself and the divisor does not exceed 44.

Current root: 12

Result: The square root of 144 is 12.

More About on Finding Square Root of a Number by Division Method

Properties of the Long Division Method for Finding Square Roots

• Incremental Precision: The method allows for incrementally improving precision, digit by digit, by repeating the calculation for as many decimal places as required.
• Works for Any Positive Number: The method can find square roots for both perfect squares and non-perfect squares, as well as for whole and decimal numbers.
• No Advanced Tools Needed: It relies purely on arithmetic operations (addition, subtraction, multiplication, and division) and requires no special tools other than paper and pencil.
• Systematic Approach: The algorithm provides a systematic approach to finding square roots, following a step-by-step process of digit pairs, estimation, and refinement.
• Applicability to Irrational Numbers: Although the result may not be exact, the Long Division method can approximate the square root of irrational numbers up to any desired level of accuracy.
• Educational Value: Practicing the Long Division method reinforces concepts in arithmetic, algebra, and number theory, enhancing understanding of numerical relationships.
• Historical Significance: This method reflects traditional mathematical techniques that have been used for centuries and are still relevant in understanding fundamental arithmetic concepts.

Examples to Finding Square Root of a Number by Division Method

Example 1: Finding the Square Root of 529

Pair the Digits: Separate 529 into pairs: 5|29.

Estimate the Largest Digit: Find the largest digit whose square is less than or equal to 5. This is 2, because 2²=4.

Current root: 2

Subtract 4 from 5 to get 1.

Bring Down the Next Pair: Bring down 29 to the right of 1 to form 129.

Double the Result: Double the current result (2) to get 4.

New divisor: 4

Find the Largest Digit for the Divisor: Find the digit to fill in the blank that, when multiplied, gives a result less than or equal to 129.

• Trying 3: 43×3 = 129Subtract 129 from 129 to get 0.

Final root: 23

The square root of 529 is 23.

Example 2: Finding the Square Root of 169

Pair the Digits: Separate 169 into pairs: 1|69.

Estimate the Largest Digit: The largest digit whose square is less than or equal to 1 is 1.

Current root: 1

Subtract 1² = 1 from 1 to get 0.

Bring Down the Next Pair: Bring down 69 to the right of 0 to form 69.

Double the Result: Double the current result (1) to get 2.

New divisor: 2

Find the Largest Digit for the Divisor: Find the digit that fills in the blank and produces a product less than or equal to 69.

• Trying 3: 23×3 = 69Subtract 69 from 69 to get 0.

Final root: 13

The square root of 169 is 13.

Example 3: Finding the Square Root of 625

Pair the Digits: Separate 625 into pairs: 6|25.

Estimate the Largest Digit: The largest digit whose square is less than or equal to 6 is 2.

Current root: 2

Subtract 2² = 4 from 6 to get 2.

Bring Down the Next Pair: Bring down 25 to the right of 2 to form 225.

Double the Result: Double the current result (2) to get 4.

New divisor: 4

Find the Largest Digit for the Divisor: Find the digit that fills in the blank and produces a product less than or equal to 225.

• Trying 5: 45×5 = 225Subtract 225 from 225 to get 0.

Final root: 25

The square root of 625 is 25.

FAQs

Can the Long Division method be applied to negative numbers?

Not directly, as square roots of negative numbers require imaginary units. However, the same logic can apply to find the modulus of complex roots.

Can the Long Division method be used for non-integer numbers?

Yes, it can handle decimals and fractions by pairing digits to the right of the decimal point, allowing calculation of square roots for both integers and non-integer numbers.

What makes the Long Division method advantageous over other methods?

It provides high accuracy and does not require advanced tools, making it ideal for situations where a calculator is unavailable and precise square root calculations are needed.