What is the square of 200?
40000
40400
40200
40100

The square of 200 is 200×200 = 40,000. This means that when you multiply 200 by itself, the result is 40,000.
The square of a number is found by multiplying the number by itself. In the case of 200, you multiply 200 by 200. This multiplication results in 40,000, which is termed as the square of 200.
The square root of 200 is approximately 14.1421. This is the number that, when multiplied by itself, gives the product 200. The square root can be calculated more precisely with tools such as calculators or specialized software.
Square Root of 200 : 14.1421
Exponential Form : 200^½ or 200^0.5
Radical Form : √200
The square root of 200 is irrational. An irrational number is a number that cannot be exactly expressed as a simple fraction, meaning its decimal form is non-terminating and non-repeating. Since 200 is not a perfect square, its square root does not result in a whole number or a simple fraction, leading to an irrational number approximately equal to 14.1421.
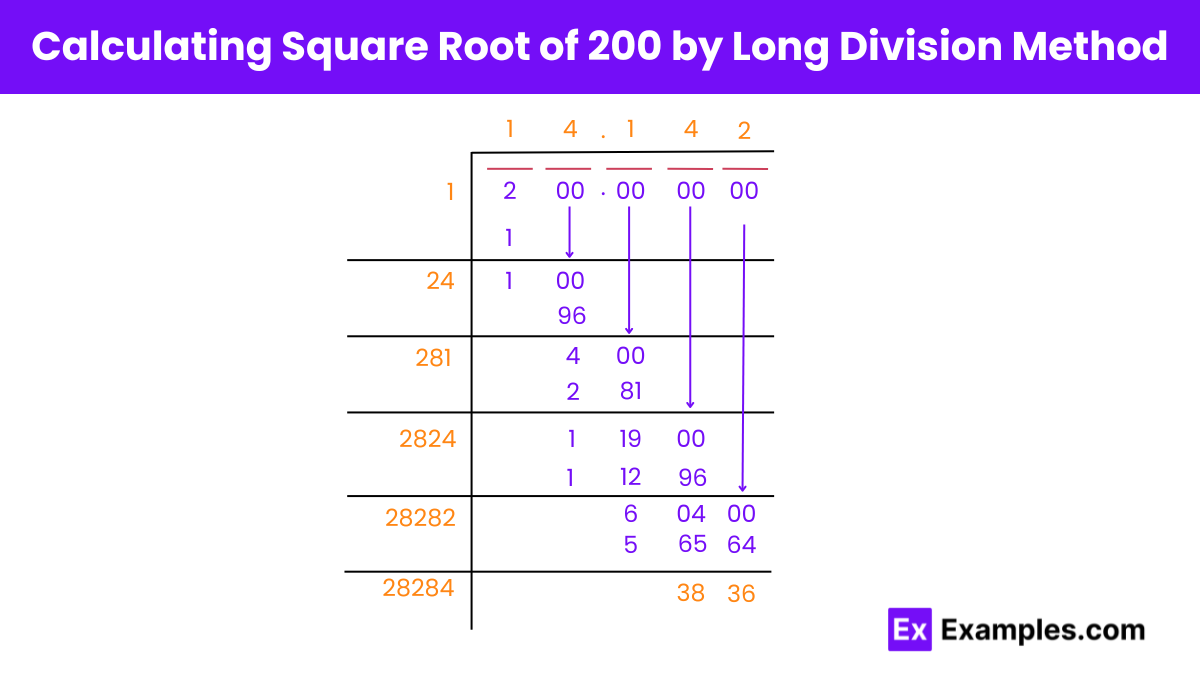
Step 1: Setup
Step 2: First Division
Step 3: Update Divisor
Step 4: Second Digit
Step 5: Third Division
Step 6: Continue the Process
Step 7: Result
No, 200 is not a perfect square. A perfect square is a number that can be expressed as the square of an integer. Since there is no whole number that, when multiplied by itself, equals 200, it cannot be considered a perfect square. For instance, the squares of the numbers immediately surrounding the square root of 200 are 142=196 and 152=225, both of which do not equal 200. Thus, 200 lacks a whole number square root and is not a perfect square.
Knowing if a number is a perfect square is important for simplifying radical expressions, solving quadratic equations, and understanding properties of geometric figures.
Yes, the square root is useful in various fields such as engineering, architecture, and physics, where calculations involving areas and resistances (in case of square laws) are necessary.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the square of 200?
40000
40400
40200
40100
Which of the following is the square root of 200 rounded to the nearest integer?
13
14
15
16
Which two consecutive whole numbers does the square root of 200 lie between?
13 and 14
14 and 15
15 and 16
12 and 13
If the square root of 200 is simplified in terms of a square root, which is it?
10√2
12√3
14√5
8√6
Which of the following is the closest approximation of the square root of 200?
14
13.5
14.1
15.5
What is the value of (√200)²?
100
200
300
400
What is 200 raised to the power of 1/2?
20
14.1
10
200
What is the decimal value of the square root of 200 to two decimal places?
14.15
14.10
14.14
14.13
C) 14.14
The square root of 200 is approximately 14.1421. Rounded to two decimal places, it is 14.14.
13 < √200 < 14
14 < √200 < 15
15 < √200 < 16
12 < √200 < 13
Which of the following is a true statement about the square of 200?
It is less than 40000
It is equal to 20000
It is greater than 40000
It is equal to 40000
Before you leave, take our quick quiz to enhance your learning!

