Square & Square Root of 320
Square & Square Root of 320
In the realm of mathematics, especially in algebraic studies, understanding squares and square roots is crucial. This grasp enriches comprehension of mathematical relationships, serving as a cornerstone for exploration. Insights into numerical behavior emerge through studying squares and square roots, aiding in analyzing complex mathematical structures.
Square of 320
In algebraic mathematics, comprehending square numbers is pivotal. The square of 320 is found by multiplying 320 by itself, yielding 102400. This process is essential for investigating mathematical properties and patterns, offering insights into number behavior within mathematical contexts.
Square Root of 320
or
√320 = 17.888 upto 3 decimals
In algebraic mathematics, the square root of 320 is significant. Computed as an irrational number, approximately equal to 17.88854381999832, it is the number whose square equals 320. Comprehending square roots enhances understanding of mathematical relationships, providing insights into numerical behavior and patterns.
Is the Square Root of 320 Rational or Irrational?
This means it cannot be expressed as a simple fraction (ratio of two integers) and its decimal representation is non-repeating and non-terminating.
A rational number is any number that can be expressed as the quotient or fraction of two integers, where the denominator is not zero.
An irrational number is any real number that cannot be expressed as a fraction of two integers and whose decimal representation goes on infinitely without repeating.
Method to Find Value of Root 320
Prime Factorization Method:
Decompose 320 into its prime factors: (320 = 2^6 × 5).
Group the prime factors in pairs: (2^3 × 2^3 × 5).
Take one factor from each pair outside the square root, and the rest remain inside.
Simplify: √320 = 2^3× √(2 × 5) = 8√10.
Estimation Method:
Find perfect squares close to 320: 18² = 324 and 17² = 289.
Since 320 is closer to 324, estimate the square root to be between 17 and 18.
Use averaging or linear interpolation to refine the estimate.
Iterative Methods:
Newton’s Method: Start with an initial guess (e.g., 16) and iteratively refine it using the formula xₙ₊₁ =1/2(xₙ + 320/xₙ).
Babylonian Method: Similar to Newton’s method but simpler, using the formula (xₙ₊₁ = 1/2(xₙ +320/xₙ) iteratively until convergence.
Using Calculator or Software:
Many calculators and mathematical software have built-in functions to compute square roots directly.
Input 320 and find the square root to get the numerical value.
Square Root of 320 by Long Division Method
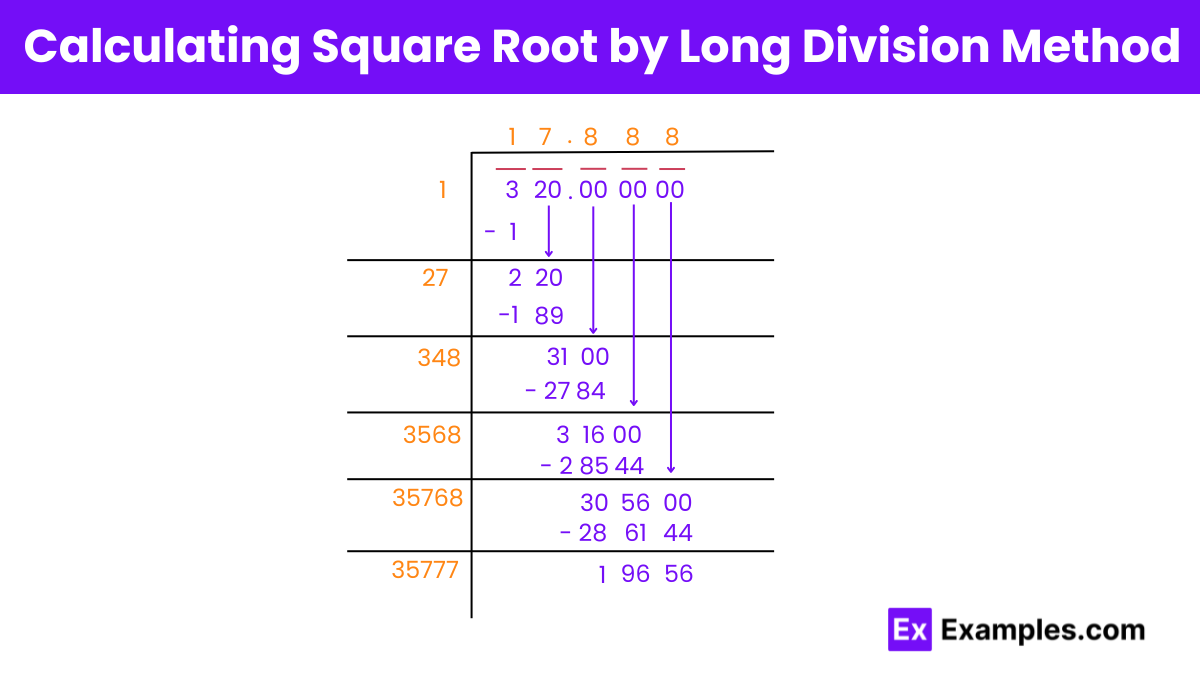
Step 1: Pair the digits of the number starting from the one’s digit by placing a bar over them as shown in the image.
Step 2:The first pair consists of only one digit, which is 3. The square of 1 is less than 3. Subtract 1 from the first pair and add the next pair as the divisor, which is 20.
Step 3: The double of 1 is 2. Now a number is placed alongside 2, making it 27. The product of 27 by 7 is 189. Subtract 189 from 220 to get a remainder of 31.
Step 4: Now double the quotient, which is 34. Add a decimal to the quotient and add a pair of zeros to the original dividend. A number alongside 34 is added, making it 348. Multiply 348 by the same number in the quotient, which is 8, resulting in 2784.
Step 5: The difference obtained is 3100 – 2784 = 316.
Step 6: Repeat the process in the same manner.
320 is Perfect Square root or Not?
A perfect square is a number that can be expressed as the square of an integer. Since 320 cannot be expressed as the square of an integer, it is not a perfect square.
FAQS
What is 320 cube root?
The cube root of 320 is approximately 7.3681.
What is the square root of 320 to the nearest whole number?
The square root of 320 to the nearest whole number is approximately 18.
What are the factors of 320?
The factors of 320 are the numbers that divide evenly into 320 without leaving a remainder. The factors of 320 are: 1, 2, 4, 5, 8, 10, 16, 20, 32, 40, 64, 80, 160, and 320.
Share :
