Value of Log 1 to 100

Team Maths - Examples.com
Created by: Team Maths - Examples.com, Last Updated: August 14, 2024

Value of Log 1 to 100

Value of Log 1 to 100.

Logarithms are mathematical functions that help to solve equations involving exponential growth or decay. The logarithm of a number is the exponent to which the base must be raised to produce that number. For instance, the logarithm of 1000 to the base 10 is 3, because 10Ā³ = 10001. In other words, logarithms can be considered as the inverse operations of exponentiation.

Understanding logarithms is essential in various fields such as mathematics, science, engineering, and computer science. A logarithm, often abbreviated as “log,” is the inverse operation to exponentiation, just as subtraction is the inverse of addition and division is the inverse of multiplication. In simpler terms, the logarithm of a number is the exponent to which the base must be raised to produce that number.

Download Value of Log 1 to 100 in PDF

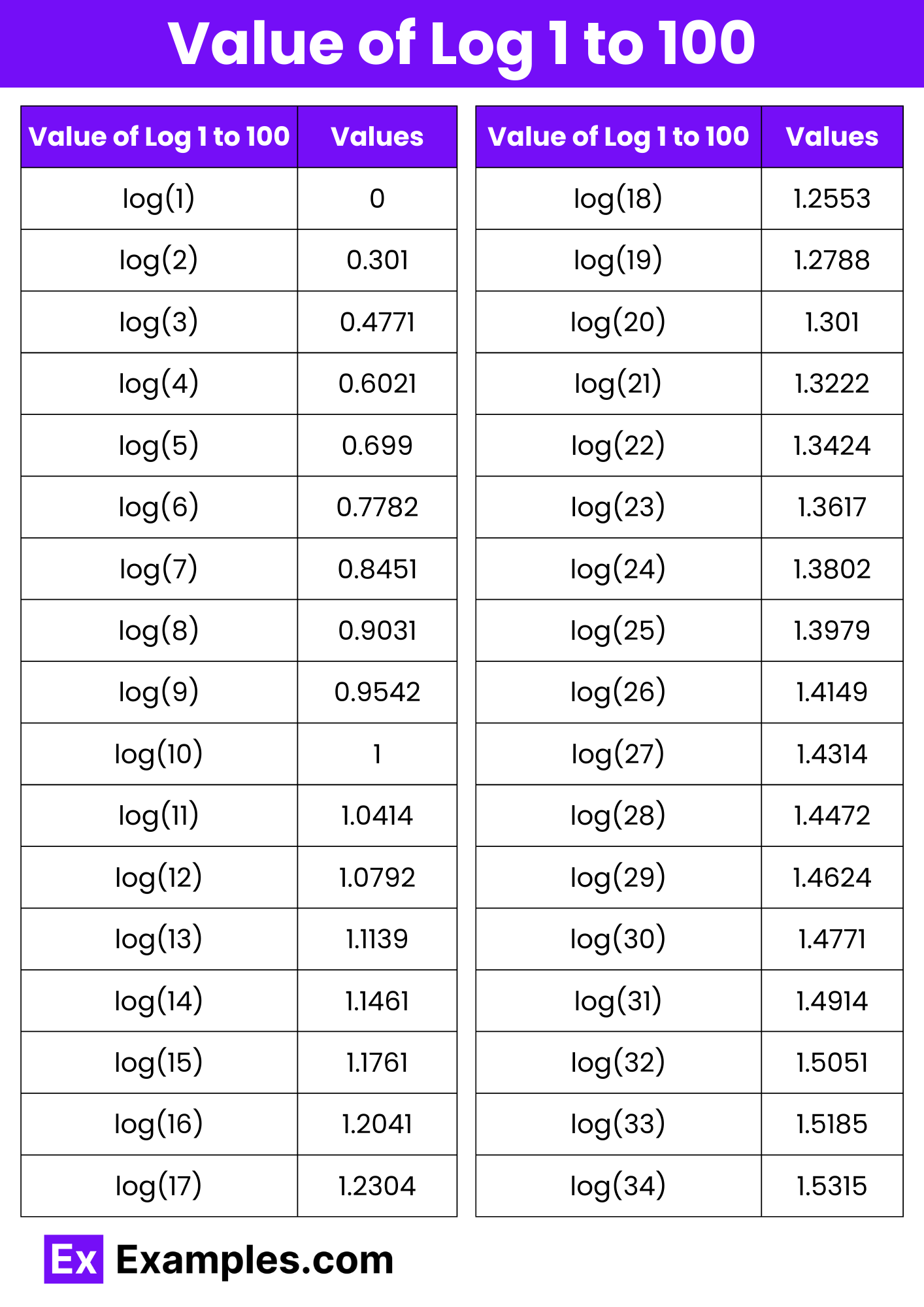
Value of Log 1 to 100

Value of Log 1 to 100

Download Value of Log 1 to 100 in PDF

Value of Log 1 to 100ValuesIn Words
log(1)0Zero
log(2)0.3010Zero point three zero one zero
log(3)0.4771Zero point four seven seven one
log(4)0.6021Zero point six zero two one
log(5)0.6990Zero point six nine nine zero
log(6)0.7782Zero point seven seven eight two
log(7)0.8451Zero point eight four five one
log(8)0.9031Zero point nine zero three one
log(9)0.9542Zero point nine five four two
log(10)1One
log(11)1.0414One point zero four one four
log(12)1.0792One point zero seven nine two
log(13)1.1139One point one one three nine
log(14)1.1461One point one four six one
log(15)1.1761One point one seven six one
log(16)1.2041One point two zero four one
log(17)1.2304One point two three zero four
log(18)1.2553One point two five five three
log(19)1.2788One point two seven eight eight
log(20)1.3010One point three zero one zero
log(21)1.3222One point three two two two
log(22)1.3424One point three four two four
log(23)1.3617One point three six one seven
log(24)1.3802One point three eight zero two
log(25)1.3979One point three nine seven nine
log(26)1.4149One point four one four nine
log(27)1.4314One point four three one four
log(28)1.4472One point four four seven two
log(29)1.4624One point four six two four
log(30)1.4771One point four seven seven one
log(31)1.4914One point four nine one four
log(32)1.5051One point five zero five one
log(33)1.5185One point five one eight five
log(34)1.5315One point five three one five
log(35)1.5441One point five four four one
log(36)1.5563One point five five six three
log(37)1.5682One point five six eight two
log(38)1.5798One point five seven nine eight
log(39)1.5911One point five nine one one
log(40)1.6021One point six zero two one
log(41)1.6128One point six one two eight
log(42)1.6232One point six two three two
log(43)1.6335One point six three three five
log(44)1.6435One point six four three five
log(45)1.6532One point six five three two
log(46)1.6628One point six six two eight
log(47)1.6721One point six seven two one
log(48)1.6812One point six eight one two
log(49)1.6902One point six nine zero two
log(50)1.6990One point six nine nine zero
log(51)1.7076One point seven zero seven six
log(52)1.7160One point seven one six zero
log(53)1.7243One point seven two four three
log(54)1.7324One point seven three two four
log(55)1.7404One point seven four zero four
log(56)1.7482One point seven four eight two
log(57)1.7559One point seven five five nine
log(58)1.7634One point seven six three four
log(59)1.7709One point seven seven zero nine
log(60)1.7782One point seven seven eight two
log(61)1.7853One point seven eight five three
log(62)1.7924One point seven nine two four
log(63)1.7993One point seven nine nine three
log(64)1.8062One point eight zero six two
log(65)1.8129One point eight one two nine
log(66)1.8195One point eight one nine five
log(67)1.8261One point eight two six one
log(68)1.8325One point eight three two five
log(69)1.8388One point eight three eight eight
log(70)1.8451One point eight four five one
log(71)1.8513One point eight five one three
log(72)1.8573One point eight five seven three
log(73)1.8633One point eight six three three
log(74)1.8692One point eight six nine two
log(75)1.8751One point eight seven five one
log(76)1.8808One point eight eight zero eight
log(77)1.8865One point eight eight six five
log(78)1.8921One point eight nine two one
log(79)1.8976One point eight nine seven six
log(80)1.9031One point nine zero three one
log(81)1.9085One point nine zero eight five
log(82)1.9138One point nine one three eight
log(83)1.9191One point nine one nine one
log(84)1.9243One point nine two four three
log(85)1.9294One point nine two nine four
log(86)1.9345One point nine three four five
log(87)1.9395One point nine three nine five
log(88)1.9445One point nine four four five
log(89)1.9494One point nine four nine four
log(90)1.9542One point nine five four two
log(91)1.9590One point nine five nine zero
log(92)1.9638One point nine six three eight
log(93)1.9685One point nine six eight five
log(94)1.9731One point nine seven three one
log(95)1.9777One point nine seven seven seven
log(96)1.9823One point nine eight two three
log(97)1.9868One point nine eight six eight
log(98)1.9912One point nine nine one two
log(99)1.9956One point nine nine five six
log(100)2.0000Two

The logarithmic values of numbers from 1 to 100 provide crucial insights in various mathematical and scientific contexts, particularly in simplifying multiplication and division into addition and subtraction. Logarithms help in understanding exponential growth, decay, and scales like the Richter scale for earthquakes and the pH scale in chemistry. They are instrumental in algorithms, data analysis, and complex calculations. Recognizing the value of logarithms for numbers 1 through 100, especially in base 10 (common logarithms) and base e (natural logarithms), enhances computational efficiency and analytical precision across numerous disciplines.

AI Generator

Text prompt

Add Tone

Select a Tone

10 Examples of Public speaking

20 Examples of Gas lighting

school Ready to Test Your Knowledge?

close

Before you leave, take our quick quiz to enhance your learning!

assessment Assess Your Mastery
emoji_events Boost Your Confidence
speed Instant Results
memory Enhance Retention
event_available Prepare for Exams
repeat Reinforce Learning
šŸ‘‰ Start the Quiz Now