What is the cube root of 8?
2
4
6
8


The cube root of a number is the value that, when multiplied by itself three times (cubed), gives the original number. Mathematically, the cube root of n is represented as ∛n. For example, the cube root of 27 is 3, because 3×3×3=27.
Below is a table that provides the cube roots of numbers from 1 to 20. Each entry includes the number and its cube root in numerical form. This representation aids in visualizing and understanding the relationship between numbers and their cube roots, fostering a deeper comprehension of the concept and its applications.
Download Cube Root 1-20 in PDF
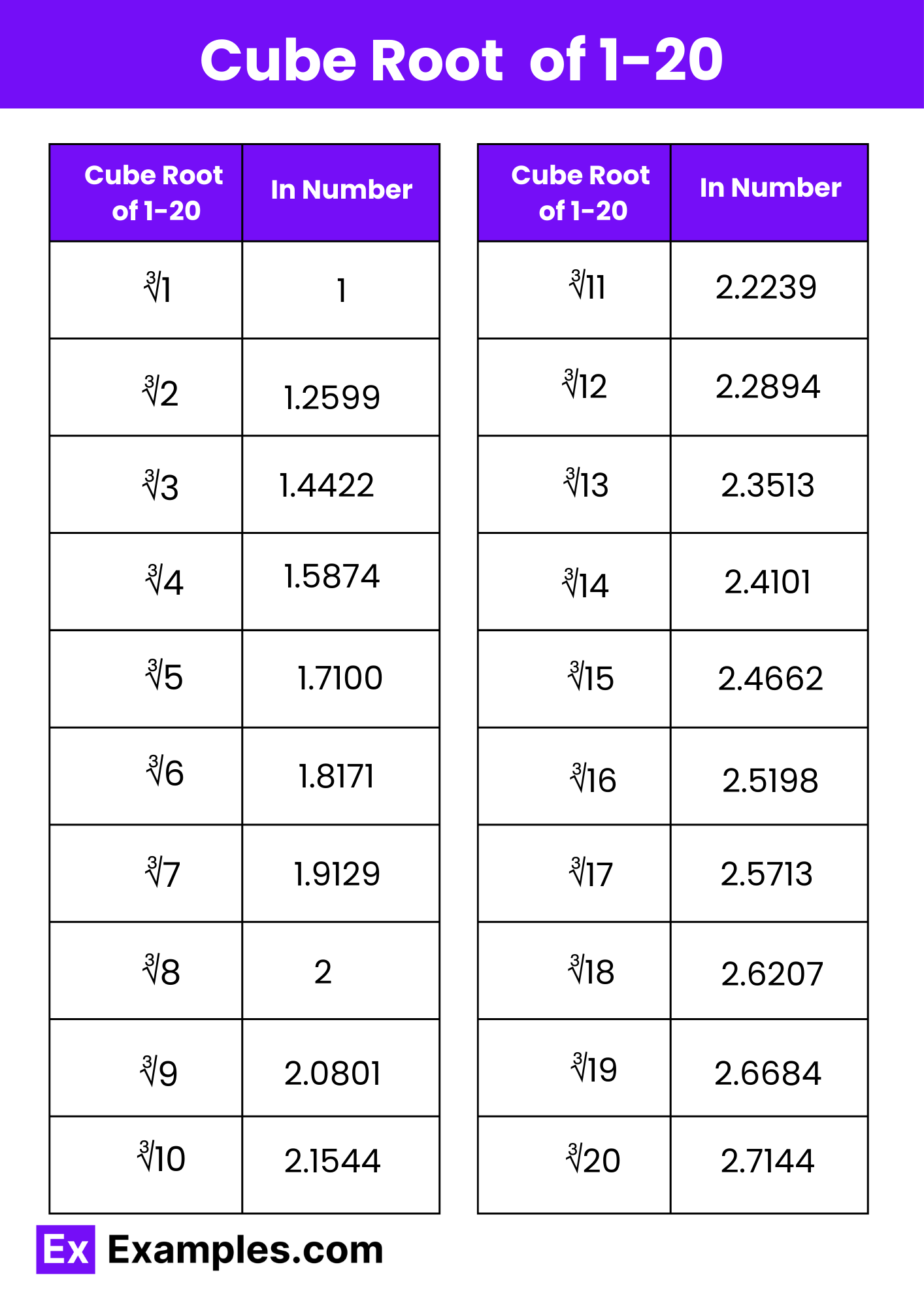
Download Cube Root 1-20 in PDF
| Cube Root of 1-20 Values | In Number | In Words |
|---|---|---|
| ∛1 | 1.0000 | One point zero zero zero zero |
| ∛2 | 1.2599 | One point two five nine nine |
| ∛3 | 1.4422 | One point four four two two |
| ∛4 | 1.5874 | One point five eight seven four |
| ∛5 | 1.7100 | One point seven one zero zero |
| ∛6 | 1.8171 | One point eight one seven one |
| ∛7 | 1.9129 | One point nine one two nine |
| ∛8 | 2.0000 | Two point zero zero zero zero |
| ∛9 | 2.0801 | Two point zero eight zero one |
| ∛10 | 2.1544 | Two point one five four four |
| ∛11 | 2.2239 | Two point two two three nine |
| ∛12 | 2.2894 | Two point two eight nine four |
| ∛13 | 2.3513 | Two point three five one three |
| ∛14 | 2.4101 | Two point four one zero one |
| ∛15 | 2.4662 | Two point four six six two |
| ∛16 | 2.5198 | Two point five one nine eight |
| ∛17 | 2.5713 | Two point five seven one three |
| ∛18 | 2.6207 | Two point six two zero seven |
| ∛19 | 2.6684 | Two point six six eight four |
| ∛20 | 2.7144 | Two point seven one four four |
Understanding the cube roots of numbers from 1 to 20 is a fundamental mathematical skill that lays the groundwork for more advanced concepts in algebra and geometry. Knowing these cube roots helps in solving cubic equations, understanding the volume of three-dimensional shapes, and analyzing real-world problems involving cubic relationships. By mastering the cube roots of these numbers, students can enhance their mathematical proficiency and prepare for more complex topics in higher mathematics. This foundational knowledge is crucial for success in various academic and professional fields that rely on mathematical reasoning and problem-solving.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the cube root of 8?
2
4
6
8
Which number has a cube root of 3?
6
9
27
40
What is the cube root of 125?
5
10
15
20
Which number has a cube root of 4?
8
12
16
64
Find the cube root of 343.
5
7
9
11
Find the cube root of 1331.
10
11
12
13
Determine the cube root of 2744.
14
15
16
17
Find the cube root of 4096.
15
16
17
18
What is the cube root of 8000?
20
21
22
23
Find the cube root of 6859.
18
19
20
21
Before you leave, take our quick quiz to enhance your learning!

