GCF of 18 and 27
GCF of 18 and 27
To determine the greatest common factor (GCF) of 18 and 27, various methods can be employed. One method is by listing common factors: for 18, the factors are 1, 2, 3, 6, 9, and 18, while for 27, they are 1, 3, 9, and 27. Among these, the largest common factor is 9. Another method is prime factorization: breaking down 18 into 2×3×3 and 27 into 3×3×3, the common prime factor is 3×3=9. Thus, regardless of the method used, the GCF of 18 and 27 remains 9, signifying the largest numbers that divides both without leaving a remainder.
GCF of 18 and 27
GCF of 18 and 27 is 9.
The greatest common factor (GCF) of 18 and 27 is 9. By listing common factors or prime factorization, 9 emerges as the largest number dividing both without remainder.
Methods to Find GCF of 18 and 27
- Prime Factorization Method
- Long Division Method
- Listing Common Factors
GCF of 18 and 27 by Prime Factorization Method
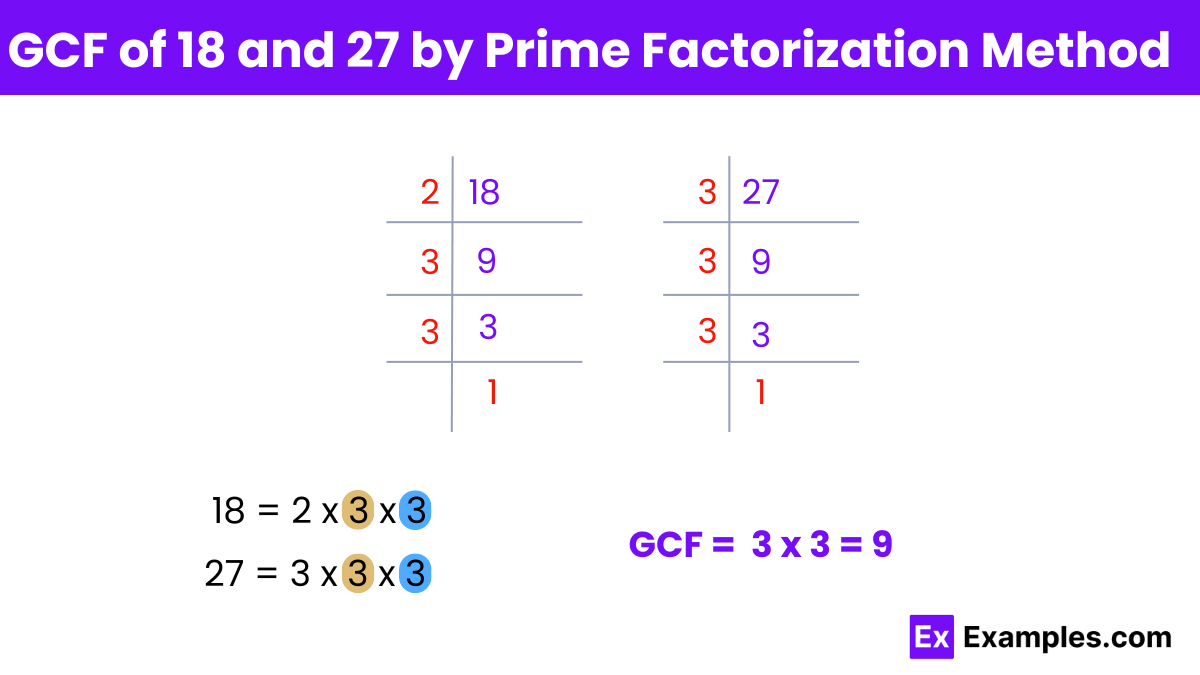
Find the prime factors of each number:
Prime factors of 18:
Divide 18 by 2 (the smallest prime number):18 ÷ 2 =9.
Next, factorize 9, which is not a prime number:9 ÷ 3 = 3.
Therefore, the prime factors of 18 are:18 = 2 × 3 × 3 or 2 × 3²
Prime factors of 27:
Divide 27 by 3 (the smallest prime number):27 ÷ 3 = 9.
Next, factorize 9, which is not a prime number:9 ÷ 3 = 3.
Therefore, the prime factors of 27 are:27 = 3 × 3 × 3 or 3³
Identify the common prime factors:
The prime factors of 18 are 2×3².
The prime factors of 27 are 3³.
The common prime factor is 3, and the smallest power of 3 in both factorizations is 3².
Multiply the common prime factors:
The GCF is found by multiplying the common prime factors with the smallest exponents :
GCF = 3² = 9
GCF of 18 and 27 by Long Division Method.
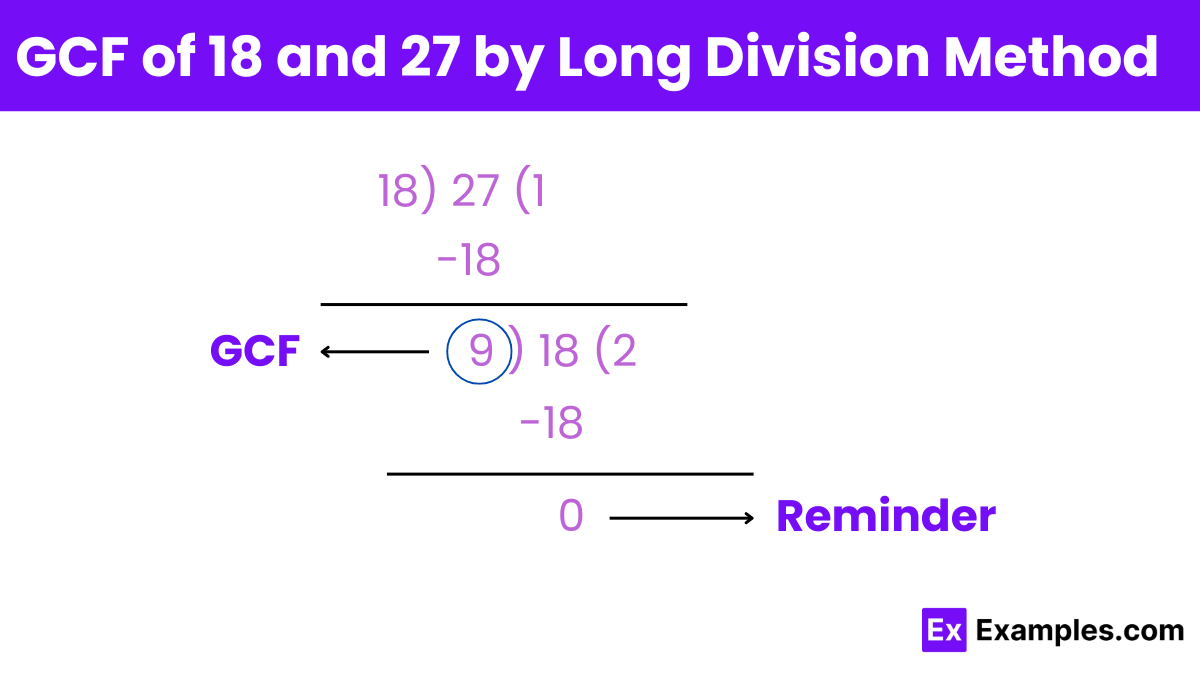
Divide the larger number by the smaller number:
- Larger number: 27
- Smaller number: 18
27 ÷ 18 = 1 (quotient) , remainder = 27 − (18×1) = 9
Replace the larger number with the smaller number and the smaller number with the remainder:
- New larger number: 18
- New smaller number: 9
Divide the new larger number by the new smaller number:
18 ÷ 9 = 2 (quotient ), remainder = 18 − (9×2) = 0
Repeat the process until the remainder is 0:
- In the second step, the remainder is 0, which means the process stops here.
The divisor at this step is the GCF:
The divisor at the last step before the remainder became 0 is 9.
GCF of 18 and 27 by Listing Common Factors
List the factors of each number:
Factors of 18: 1, 2, 3, 6, 9, 18
Factors of 27: 1, 3, 9, 27
Identify the common factors:
The common factors of 18 and 27 are: 1, 3, 9
Determine the greatest common factor:
- Among the common factors, the largest one is 9.
Why is finding the GCF important?
The GCF is useful for simplifying fractions, dividing quantities evenly, and solving problems involving ratios.
Can the GCF be larger than the smallest number?
No, the GCF cannot be larger than the smallest of the given numbers.
How can understanding GCF benefit students in math?
Understanding GCF helps students simplify fractions, solve problems involving divisors, and enhance their number theory skills.
What is the GCF of 18 and 27 used for in real life?
The GCF can be used for reducing fractions, dividing items into equal groups, and solving problems in finance, engineering, and computer science.
Can the GCF be found for negative numbers?
Yes, the GCF can be found for negative numbers. The GCF of -18 and 27 is the same as the GCF of 18 and 27, which is 9. The GCF is always a positive number.
Share :
