GCF of 35 and 50
GCF of 35 and 50
The Greatest Common Factor (GCF) of 35 and 50 is 5. This is determined by identifying the common prime factors of the two numbers. The prime factorization of 35 is 5 × 7, and the prime factorization of 50 is 2 × 5 × 5. The only common prime factor is 5, making it the GCF of 35 and 50.
GCF of 35 and 50
GCF of 35 and 50 is 5.
Methods to Find GCF of 35 and 50
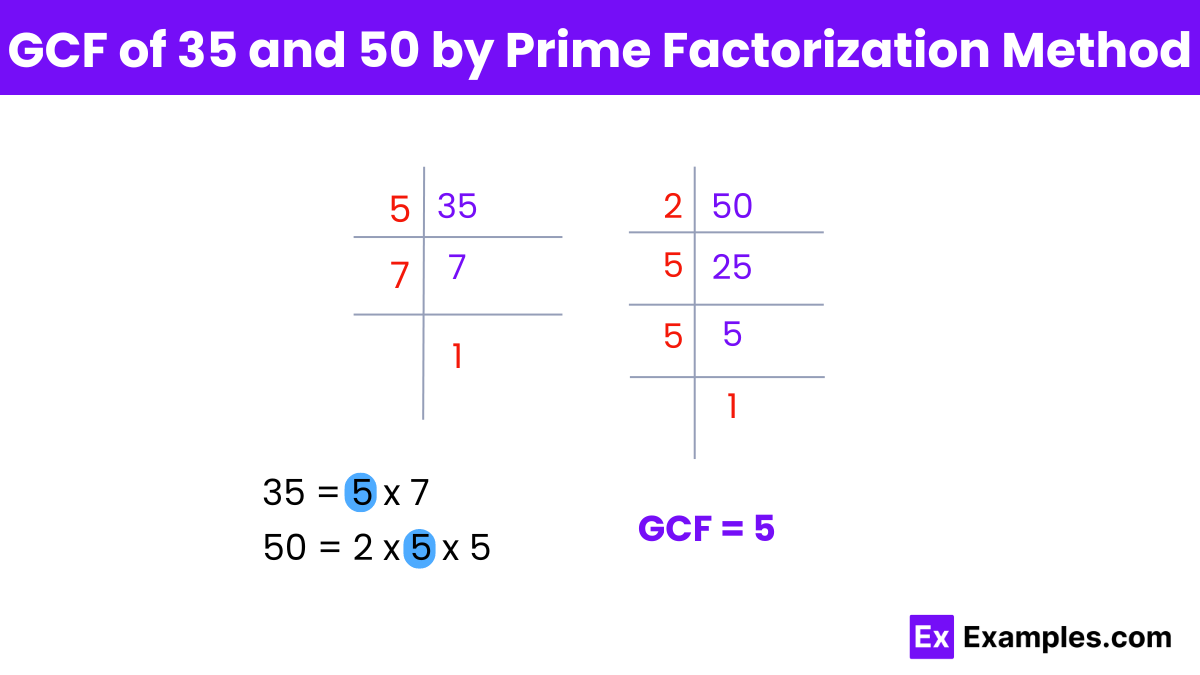
- Prime Factorization Method
- Long Division Method
- Listing Common Factors
GCF of 35 and 50 by Prime Factorization Method
Prime Factorization of 35:
- 35 = 5 × 7
Prime Factorization of 50:
- 50 = 2 × 5 × 5 (or 2×5²)
Identify Common Factors:
- The common prime factor between 35 and 50 is 5.
Determine the GCF:
Since the only common prime factor is 5, the GCF of 35 and 50 is 5.
GCF of 35 and 50 by Long Division Method.
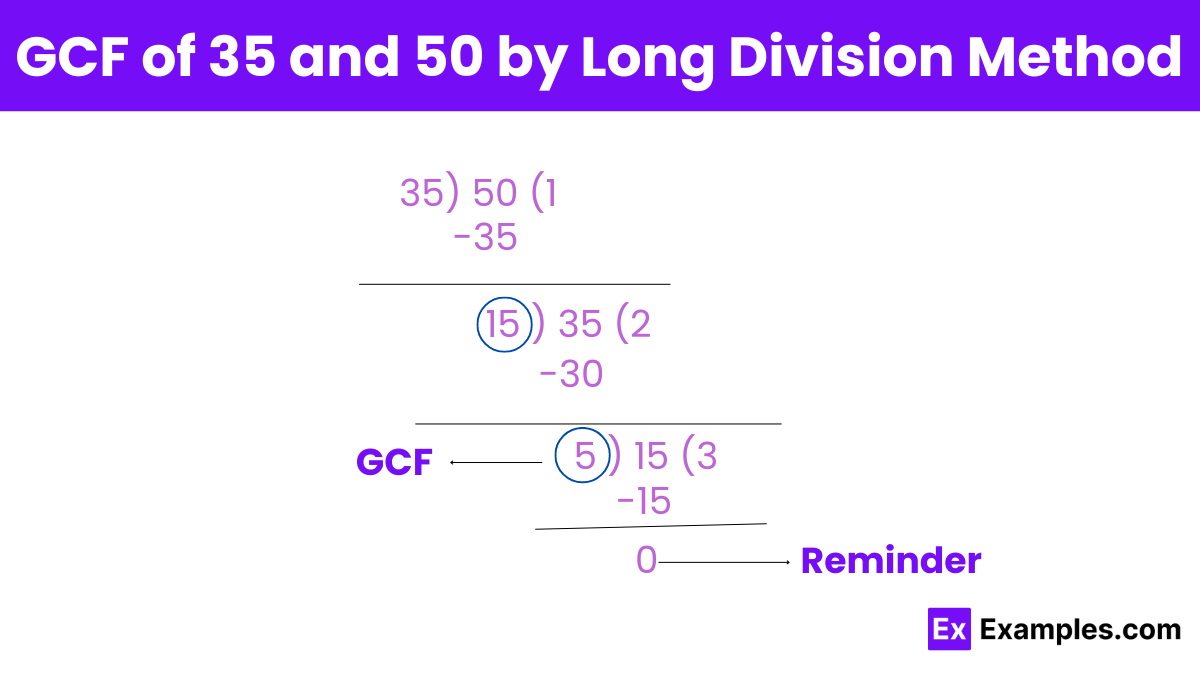
Divide the larger number (50) by the smaller number (35):
50 ÷ 35 gives a quotient of 1 and a remainder of 15.
Replace the larger number with the smaller number (35) and the smaller number with the remainder (15):
Now, divide 35 by 15.
35 ÷ 15 gives a quotient of 2 and a remainder of 5.
Repeat the process: Replace 35 with 15 and 15 with the remainder 5.
Now, divide 15 by 5.
15 ÷ 5 gives a quotient of 3 and a remainder of 0.
When the remainder is 0, the divisors at this step is the GCF.
So, the GCF of 35 and 50 is 5.
GCF of 35 and 50 by Listing Common Factors
List the factors of 35:
Factors of 35: 1, 5, 7, 35
List the factors of 50:
Factors of 50: 1, 2, 5, 10, 25, 50
Identify the common factors:
Common factors of 35 and 50: 1, 5
Determine the greatest common factor:
The greatest common factor is 5.
Therefore, the GCF of 35 and 50 is 5.
What is the GCF of 35 and 50?
The GCF (Greatest Common Factor) of 35 and 50 is 5.
Why is the GCF of 35 and 50 important?
The GCF is important in simplifying fractions, solving problems involving ratios, and finding common denominators.
Can the GCF of 35 and 50 be greater than 5?
No, the GCF of 35 and 50 cannot be greater than 5 because 5 is the largest number that divides both 35 and 50 without leaving a remainder.
How is the GCF of 35 and 50 used in real-life situations?
The GCF is used in real-life situations such as dividing items into smaller sections, comparing quantities, and simplifying mathematical problems involving fractions.
Can the GCF of 35 and 50 be found using a calculator?
Yes, many calculators have a function to find the GCF of two numbers. Simply input the numbers 35 and 50 and use the GCF or GCD function.
Share :
