GCF of 6 and 15
GCF of 6 and 15
The Greatest Common Factor (GCF) of 6 and 15 is the largest number that divides both numbers without leaving a remainder. To determine this, we can list the factors of each number: for 6, the factors are 1, 2, 3, and 6, while for 15, the factors are 1, 3, 5, and 15. The common factors between 6 and 15 are 1 and 3. The largest of these common factors is 3. Therefore, the GCF of 6 and 15 is 3, which is useful for simplifying fractions and solving problems involving these numbers.
GCF of 6 and 15
GCF of 6 and 15 is 3.
Methods to Find GCF of 6 and 15
- Prime Factorization Method
- Long Division Method
- Listing Common Factors
GCF of 6 and 15 by Prime Factorization Method.
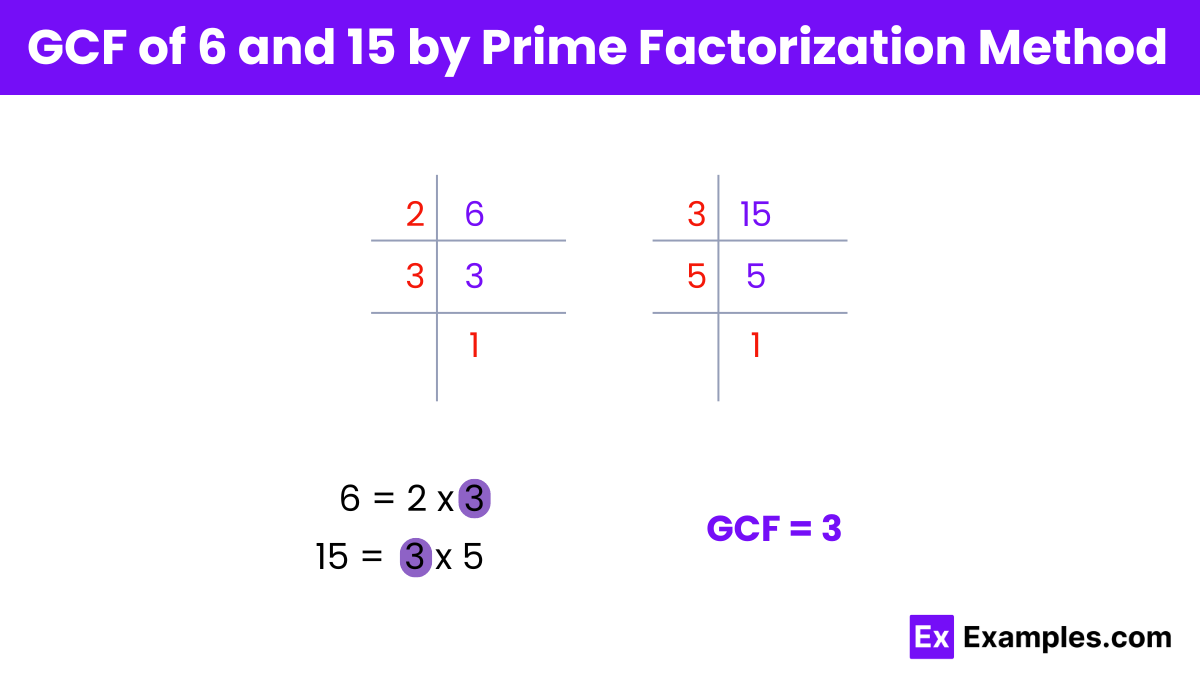
To find the Greatest Common Factor (GCF) of 6 and 15 using the prime factorization method, follow these steps:
Step-by-Step Process:
Prime Factorization of Each Number:
Prime factors of 6:
6 = 2 × 3
Prime factors of 15:
15 = 3 × 5
Identify the Common Prime Factors:
The only common prime factor is 3.
Multiply the Common Prime Factors:
GCF = 3
GCF of 6 and 15 by Long Division Method.
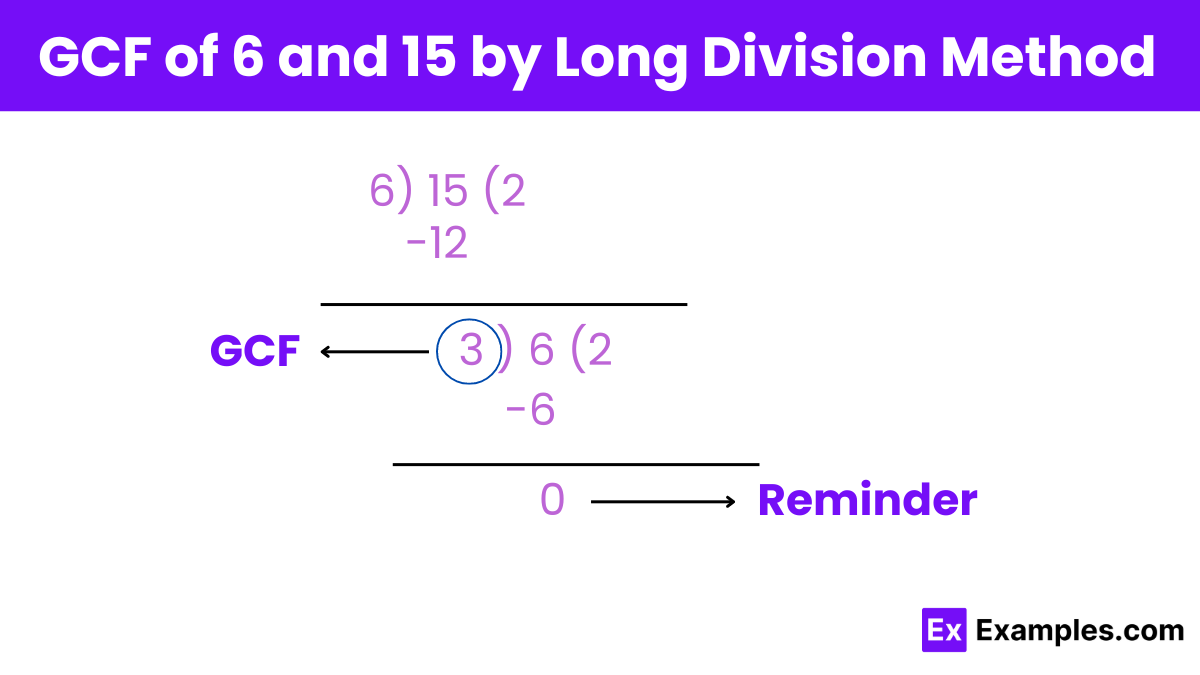
To find the Greatest Common Factor (GCF) of 6 and 15 using the Long Division Method, follow these steps:
Step-by-Step Process:
Divide the Larger Number by the Smaller Number:
Divide 15 (larger number) by 6 (smaller number).
15 ÷ 6 = 2 remainder 3
Replace the Larger Number with the Smaller Number:
The divisor (6) becomes the new dividend.
The remainder (3) becomes the new divisor.
Repeat the Division:
Now, divide 6 by 3.
6 ÷ 3 = 2 remainder 0
Check the Remainder:
When the remainder is 0, the current divisors is the GCF.
The remainder is 0, and the current divisor is 3.
GCF of 6 and 15 by Listing Common Factors.
To find the Greatest Common Factor (GCF) of 6 and 15 by listing their common factors, follow these steps:
Step-by-Step Process:
List the Factors of Each Number:
Factors of 6: 1, 2, 3, 6
Factors of 15: 1, 3, 5, 15
Identify the Common Factors:
The common factors of 6 and 15 are: 1, 3
Find the Greatest Common Factor:
The largest number in the list of common factors is 3.
Is there a formula for finding the GCF of 6 and 15?
There isn’t a single formula, but methods like prime factorization, listing factors, and the Euclidean algorithm are used to find the GCF.
How do you find the GCF of multiple numbers, including 6 and 15?
Find the GCF of two numbers first, then use that result to find the GCF with the next number, continuing until all numbers are included.
What is the significance of the GCF in number theory?
In number theory, the GCF is fundamental for understanding the relationships between numbers, particularly in modular arithmetic and divisibility.
Can the GCF be used in real-world applications like construction?
Yes, the GCF helps in determining the optimal dimensions for dividing materials and resources evenly in construction and other fields.
Why is understanding the GCF important in mathematics?
Understanding the GCF is crucial for simplifying expressions, solving equations, and working with ratios and proportions effectively.
Is the GCF the same as the greatest common divisor (GCD)?
Yes, the Greatest Common Factor (GCF) is also known as the Greatest Common Divisor (GCD).
Share :
