Sets
What is Set?
A set is a collection of well-defined and distinct objects or elements. For instance, the collection of vowels forms a set, as they are clearly defined as “a, e, i, o, u.” Similarly, whole numbers and prime numbers are examples of sets, as their members are uniquely identifiable and consistent.
Types of Sets
- Finite Set: A set with a specific number of elements. For example, the set of vowels in the English alphabet, {𝑎,𝑒,𝑖,𝑜,𝑢}, is a finite set with five elements.
- Infinite Set: A set that has an unlimited number of elements. An example is the set of natural numbers, {1,2,3,4,…}, which goes on infinitely.
- Empty Set (Null Set): A set that has no elements. It’s denoted by ∅ or {}. For instance, the set of even numbers that are also odd, which is ∅ because no number can be both.
- Singleton Set: A set that contains only one element. For example, the set containing only the number 7, {7}, is a singleton set.
- Subset: A set that consists of elements all drawn from another set. For example,{1,2} is a subset of the set {1,2,3,4}.
- Power Set: The set of all subsets of a given set. For example, the power set of {1,2} is {∅,{1},{2},{1,2}}
- Disjoint Sets: Two sets that have no elements in common. For instance, {1,2,3} and {4,5,6} are disjoint sets.
- Equal Sets: Two sets that have the same elements, regardless of order or repetition. For example,{a,b,c} and {c,b,a} are equal sets.
- Complementary Sets: For a given universal set U and a subset A of U, the complement of A (denoted as Ac) consists of all elements in U that are not in A. For instance, if U={1,2,3,4,5} and A={1,3,5}, then the complement of A is Aᶜ={2,4}.
- Ordered Sets: Sets where the order of elements matters. For example, the set {1,2,3} is different from the set {3,2,1} if they’re considered as ordered sets.
- Multiset: A set where elements can repeat. For instance, a multiset could be represented as {a,a,b,c}, indicating two instances of the letter ‘a’.
Sets in Maths Examples
- Natural Numbers (N): The set of positive integers starting from 1. It’s represented as{1,2,3,…}.
- Whole Numbers (W): The set of non-negative integers, including 0. It’s represented as {0,1,2,3,…}.
- Integers (Z): The set of all positive and negative whole numbers, including 0. It’s represented as{…,−3,−2,−1,0,1,2,3,…}.
- Rational Numbers (Q): The set of numbers that can be expressed as a fraction p/q, where p and q are integers and q≠0.
- Irrational Numbers (′Q′): The set of numbers that cannot be expressed as a rational number, such as √2 or π.
- Real Numbers (R): The set that encompasses both rational and irrational numbers, represented as ′Q∪Q′. It covers all points on the number line.
Operations on Sets
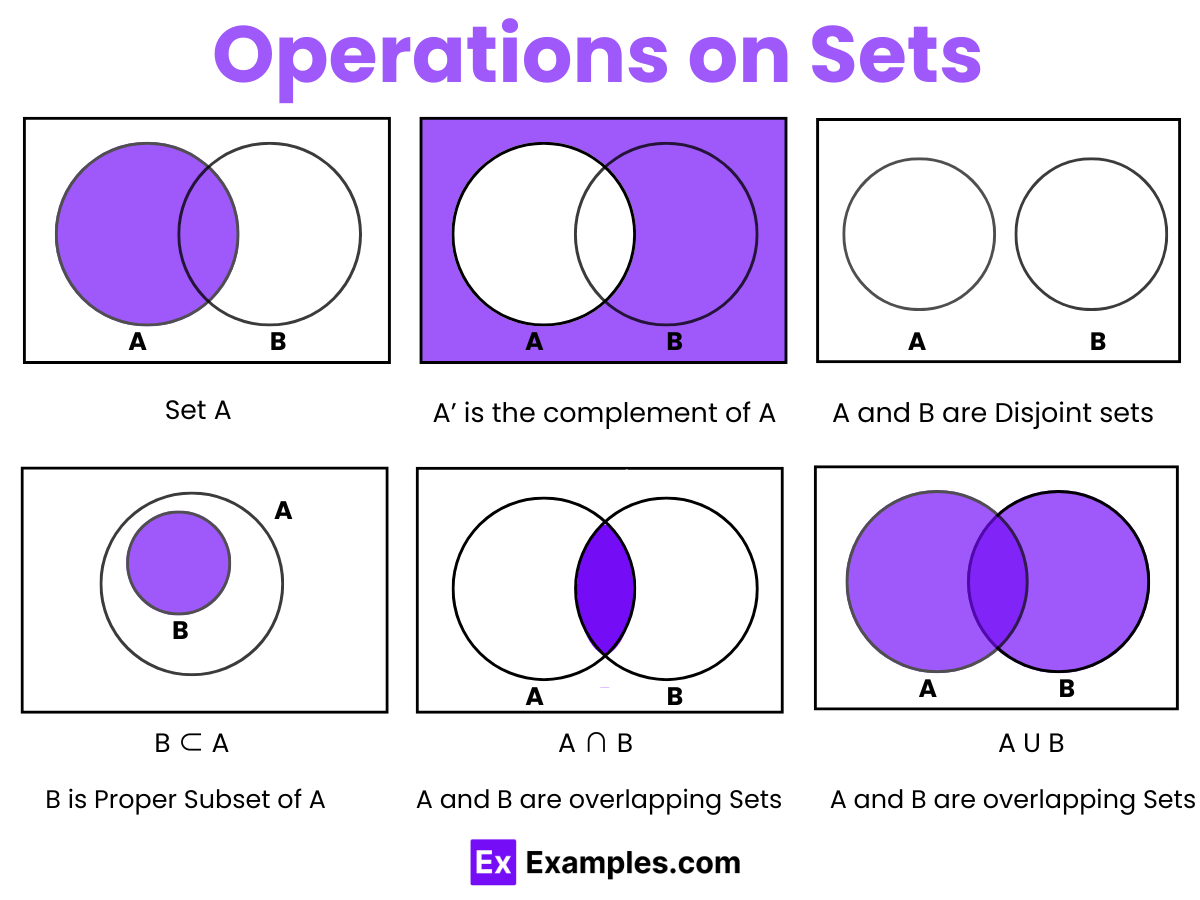
Operations on sets are fundamental ways to manipulate and combine sets, providing powerful tools in mathematics and computer science. Here are key set operations:
- Union: The union of two sets A and B (denoted A∪B) includes all elements that are in A, B, or both. For example, if A={1,2,3} and B={3,4,5}, then A∪B={1,2,3,4,5}.
- Intersection: The intersection of two sets A and B (denoted A∩B) consists of all elements that are in both A and B. For example, if A={1,2,3} and B={3,4,5}, then A∩B={3}.
- Difference: The difference of two sets A and B (denoted A−B) includes elements that are in A but not in B. For example, if A={1,2,3} and B={3,4,5}, then A−B={1,2} And B−A={4,5}.
- Symmetric Difference: The symmetric difference of two sets A and B (denoted A△B) consists of elements that are in A or B, but not both. For example, if A={1,2,3} and B={3,4,5}, then A△B={1,2,4,5}.
- Complement: The complement of a set A (denoted Aᶜ) consists of all elements that are not in A but are in the universal set U. For example, if U={1,2,3,4,5} and A={1,2,3}, then Ac={4,5}.
- Cartesian Product: The Cartesian product of two sets A and B (denoted A×B) consists of all ordered pairs (a,b) where a∈A and b∈B. For example,A={1,2} and 𝐵={3,4}, then 𝐴×𝐵={(1,3),(1,4),(2,3),(2,4)}.
Sets Formulas
| Formula | Description |
|---|---|
| (A∪B)∪C=A∪(B∪C) | Associative Law (Union): Union operation is associative, meaning grouping order doesn’t matter. |
| (A∩B)∩C=A∩(B∩C) | Associative Law (Intersection): Intersection operation is associative. |
| A∪(B∩C)=(A∪B)∩(A∪C) | Distributive Law (Union over Intersection): Union distributes over intersection. |
| A∩(B∪C)=(A∩B)∩(A∩C) | Distributive Law (Intersection over Union): Intersection distributes over union. |
| (A∪B∪C)ᶜ=Aᶜ∩Bᶜ∩Cᶜ | De Morgan’s Law (Union): The complement of a union is the intersection of the complements. |
| (A∩B∩C)ᶜ=Aᶜ∪Bᶜ∪Cᶜ | De Morgan’s Law (Intersection): The complement of an intersection is the union of the complements. |
| A∪B=B∪A | Commutative Law (Union): Union operation is commutative. |
| A∩B=B∩A | Commutative Law (Intersection): Intersection operation is commutative. |
Here are some key formulas and properties involving three sets A, B, and C:
1.Associative Law (Union): It indicates that the union operation is associative, meaning the grouping order of the sets does not matter.
(A∪B)∪C=A∪(B∪C)
2. Associative Law (Intersection): It indicates that the intersection operation is associative.
(A∩B)∩C=A∩(B∩C)
3. Distributive Law (Union over Intersection): It shows how union distributes over intersection.
A∪(B∩C)=(A∪B)∩(A∪C)
4. Distributive Law (Intersection over Union): This shows how intersection distributes over union.
A∩(B∪C)=(A∩B)∩(A∩C)
5. De Morgan’s Law (Union): This shows the complement of a union is the intersection of the complements.
(A∪B∪C)ᶜ=Aᶜ∩Bᶜ∩Cᶜ
6. De Morgan’s Law (Intersection): This shows the complement of an intersection is the union of the complements.
(A∩B∩C)ᶜ=Aᶜ∪Bᶜ∪Cᶜ
7. Commutative Law (Union): This indicates that the union operation is commutative.
A∪B =B∪A
8. Commutative Law (Intersection): This indicates that the intersection operation is commutative.
A∩B=B∩A
| Formula Expression | Description |
|---|---|
| n(A∪B)=n(A)+n(B)−n(A∩B) | Calculates the number of elements in the union of two sets A and B by adding their individual sizes and subtracting the size of their intersection. |
| n(A∪B)=n(A)+n(B) <br> If 𝐴∩𝐵=∅ | If sets A and B are disjoint (no common elements), the size of their union is simply the sum of their sizes. |
| n(A−B)+n(A∩B)=n(A) | The size of set A can be determined by adding the size of the difference of A and B to the size of their intersection. |
| n(B−A)+n(A∩B)=n(B) | Similarly, the size of set B is the sum of the size of the difference of B and A and the size of their intersection. |
| n(A−B)+n(A∩B)+n(B−A)=n(A∪B) | The total number of elements in the union of A and B can be found by adding the sizes of the differences and their intersection. |
| n(A∪B∪C)=n(A)+n(B)+n(C)−n(A∩B)−n(B∩C)−n(C∩A)+n(A∩B∩C) | This formula calculates the number of elements in the union of three sets A, B, and C by considering all possible intersections to avoid over-counting elements present in multiple sets. |
Properties of Sets
| Commutative Property : A∪B = B∪A A∩B = B∩A |
| Associative Property : A ∪ ( B ∪ C) = ( A ∪ B) ∪ C A ∩ ( B ∩ C) = ( A ∩ B) ∩ C |
| Distributive Property : A ∪ ( B ∩ C) = ( A ∪ B) ∩ (A ∪ C) A ∩ ( B ∪ C) = ( A ∩ B) ∪ ( A ∩ C) |
| De morgan’s Law : Law of union : ( A ∪ B )’ = A’ ∩ B’ Law of intersection : ( A ∩ B )’ = A’ ∪ B’ |
| Complement Law : A ∪ A’ = A’ ∪ A =UA ∩ A’ = ∅ |
| Idempotent Law And Law of a null and universal set : For any finite set A A ∪ A = A A ∩ A = A ∅’ = U ∅ = U’ |
Representation of Sets in Set Theory
In set theory, various notations are used to represent sets, each offering a unique way to list elements:
- Semantic Form: This notation describes sets by their defining properties. For example, the set of natural numbers greater than 3 can be written as {𝑥∣𝑥∈𝑁 and 𝑥>3}.
- Roster Form: This notation lists all elements of a set explicitly, separated by commas and enclosed in curly brackets. For instance, the set of vowels can be represented as {𝑎,𝑒,𝑖,𝑜,𝑢}.
- Set Builder Form: This notation defines a set by a rule or condition that its elements satisfy. For example, the set of even integers can be written as {𝑥∣𝑥 is an integer and 𝑥%2=0}.
| Set of first five even natural numbers | ||
|---|---|---|
| Semantic Form | Roster Form | Set Builder Form |
| A set of first five even natural numbers | {2, 4, 6, 8, 10} | {x ∈ ℕ | x ≤ 10 and x is even} |
Visual Representation of Sets Using Venn Diagram
A Venn Diagram is a visual representation of sets, with each set shown as a circle. The elements of a set are placed inside its respective circle. Often, the circles are enclosed by a rectangle, which represents the universal set. Venn diagrams illustrate how sets relate to one another by showing intersections, unions, and differences, making them a powerful tool for understanding set operations and relationships.
Sets Symbols
| Symbol | Meaning |
|---|---|
| ∈ | Indicates membership of an element in a set. For example, 𝑎∈𝐴 means 𝑎a is an element of set A. |
| ∉ | Indicates that an element is not a member of a set. For example, 𝑏∉𝐵 means b is not in set B. |
| ⊆ | Indicates that set A is a subset of set B (i.e., all elements of A are in B). |
| ⊂ | Indicates that set A is a proper subset of set B (i.e., all elements of A are in B and B has other elements not in A). |
| ∩ | Represents the intersection of two sets, which includes elements common to both sets. |
| ∪ | Represents the union of two sets, which includes all elements that are in either set. |
| − | Represents the difference between two sets A and B, including elements that are in A but not in B. |
| △ | Represents the symmetric difference between two sets, including elements that are in one set or the other, but not both. |
| ∅ | Represents the empty set, which contains no elements. |
| × | Represents the Cartesian product of two sets, which consists of all ordered pairs formed by elements from both sets. |
| 𝐴𝑐 | Represents the complement of set A, which includes all elements not in A but in the universal set U. |
- Question: Define a set and give an example of a finite set.
Answer: A set is a collection of distinct and well-defined objects. An example of a finite set is the set of vowels in the English alphabet: {a,e,i,o,u}, which contains five elements. - Question: What is the difference between a union and an intersection of two sets?
Answer: The union of two sets A and B (denoted A∪B) consists of all elements that are in either set or both. The intersection of two sets A and B (denoted A∩B) includes only the elements that are in both sets. - Question: How do you represent a set using set builder notation, and give an example?
Answer: Set builder notation defines a set by specifying a condition or property that its elements must satisfy. An example is the set of even integers, which can be represented as {𝑥∣𝑥 is an integer and 𝑥%2=0}. - Question: Explain the complement of a set and provide an example.
Answer: The complement of a set A (denoted 𝐴ᶜ) consists of all elements not in 𝐴 but present in the universal set U. For instance, if U={1,2,3,4,5} and 𝐴={1,3,5}, then 𝐴ᶜ={2,4}. - Question: What is the Cartesian product of two sets A and B and how is it represented?
Answer: The Cartesian product of two sets A and B (denoted 𝐴×𝐵) consists of all ordered pairs (a,b) where 𝑎∈𝐴 and 𝑏∈𝐵. For example, if 𝐴={1,2} and 𝐵={3,4}, then 𝐴×𝐵={(1,3),(1,4),(2,3),(2,4)}. - Question: What is the symmetric difference between two sets 𝐴 and 𝐵, and how is it represented?
- Answer: The symmetric difference between two sets 𝐴 and 𝐵(denoted 𝐴△𝐵) includes elements that are in one set or the other, but not both. For example, if 𝐴={1,2,3}= and 𝐵={3,4,5}, then 𝐴△𝐵={1,2,4,5}.
Question 1:
Given three sets A,B, and C such that 𝐴={1,2,3,4,5}, 𝐵={3,4,5,6,7}, and 𝐶={5,6,7,8,9}, answer the following:
- Find 𝐴∩𝐵∩𝐶(the intersection of the three sets).
- Calculate 𝐴∪𝐵∪𝐶 (the union of the three sets).
- Determine (𝐴−𝐵)∪(𝐵−𝐴)(the symmetric difference between 𝐴 and 𝐵).
Answer:
- Intersection 𝐴∩𝐵∩𝐶: The intersection includes elements that are common to all three sets:𝐴∩𝐵∩𝐶={5}
- Union 𝐴∪𝐵∪𝐶: The union includes all elements that are in any of the three sets:𝐴∪𝐵∪𝐶={1,2,3,4,5,6,7,8,9}
- Symmetric Difference (𝐴−𝐵)∪(𝐵−𝐴): This includes elements that are in 𝐴 but not in 𝐵 and vice versa:(𝐴−𝐵)∪(𝐵−𝐴)={1,2,6,7}
Question 2:
Let sets 𝐴 and 𝐵 be defined as follows:
𝐴={𝑥∣𝑥 is an integer, and 1≤𝑥≤10}
𝐵={𝑥∣𝑥 is an integer, and 5≤𝑥≤15}
- Find the elements of sets 𝐴 and 𝐵.
- Determine 𝑛(𝐴∩𝐵) (the cardinality of the intersection of 𝐴 and 𝐵).
- Find 𝑛(𝐴∪𝐵) (the cardinality of the union of 𝐴 and 𝐵).
Answer:
- Elements of A and B: 𝐴={1,2,3,4,5,6,7,8,9,10}, 𝐵={5,6,7,8,9,10,11,12,13,14,15}
- Cardinality of the Intersection 𝑛(𝐴∩𝐵): The intersection consists of elements common to both sets:𝐴∩𝐵={5,6,7,8,9,10}Therefore, the cardinality of this set is:𝑛(𝐴∩𝐵)=6
- Cardinality of the Union 𝑛(𝐴∪𝐵)n(A∪B): The union includes all unique elements in both sets:𝐴∪𝐵={1,2,3,4,5,6,7,8,9,10,11,12,13,14,15}Therefore, the cardinality of this set is: 𝑛(𝐴∪𝐵)=15
FAQ’s
What is the formula for sets?
The formula 𝑛(𝐴∪𝐵)=𝑛(𝐴)+𝑛(𝐵)−𝑛(𝐴∩𝐵) calculates the number of elements in the union of two sets by adding their individual sizes and subtracting the size of their intersection, avoiding double counting.
What is a set in maths?
In mathematics, a set is a collection of distinct and well-defined elements, such as numbers, letters, or symbols. Sets are fundamental to various mathematical concepts and operations, providing a structure for organizing and manipulating elements in disciplines like algebra and logic.
Why is the null set called a set?
A null set, or empty set, is called a set because it adheres to the definition of a set—a collection of distinct, well-defined elements. In this case, it is a set with no elements, but still conforms to set properties.
What is z in sets?
In set notation, Z denotes the set of all integers, encompassing positive, negative, and zero integers. This notation is derived from the German word “Zahlen,” meaning numbers, and is widely used in mathematical contexts.
What is a unit set?
A unit set, also known as a singleton set, contains only one element. For example, the set A={7} is a unit set because it has a single, distinct element, which makes it unique compared to sets with multiple elements.
Share :
