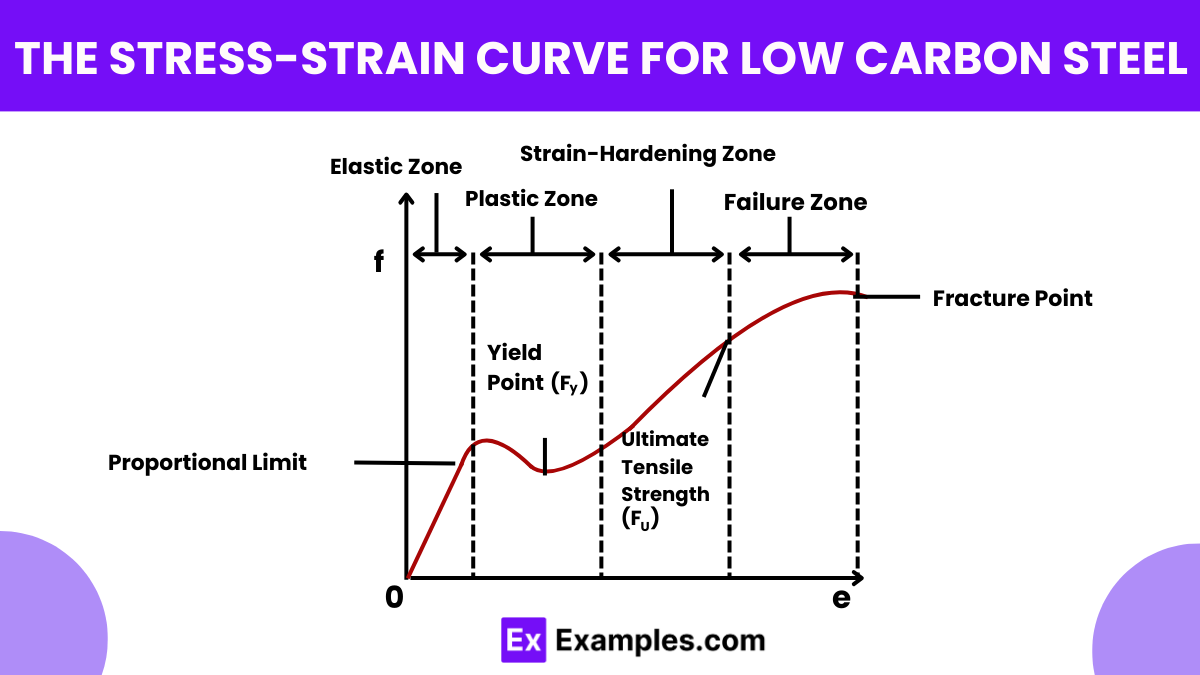
What does Hooke’s Law state about the relationship between the force applied to a spring and the extension of the spring?
Force is inversely proportional to extension
Force is directly proportional to extension
Force is equal to the square of the extension
Force is independent of the extension