Saha Ionization Equation

The Saha Ionization Equation, a fundamental concept in the laws of atomic and molecular physics, quantifies the degree of ionization of gases under equilibrium conditions based on temperature and pressure. It integrates physics principles, including thermodynamics and quantum mechanics, to predict how atoms ionize in stellar atmospheres and other plasmas, illuminating crucial aspects of the laws of physics as they apply to astrophysical phenomena.

What Is Saha Ionization Equation?

The Saha Ionization Equation is a pivotal tool in physics that describes how the ionization state of gases depends on the temperature and pressure. This equation explains the equilibrium between electrons, ions, and neutral atoms in a plasma, particularly highlighting how conditions like temperature influence ionization rates. Essentially, it enables astronomers to interpret the physical conditions of stars and nebulae by relating the degree of ionization to the environmental factors.

Saha Ionization Equation Formula

The Saha Ionization Equation formula is given by:

𝑁ᵢ𝑁ₑ/𝑁ᵢ ₋ ₁=(2𝜋𝑚ₑ𝑘𝑇)3^2/ℎ³2𝑍ᵢ/𝑍ᵢ ₋ ₁𝑒⁻ᴱᵢ/ᴷᵀ

Where:

• 𝑁ᵢ is the number of atoms in the ionization state 𝑖,
• 𝑁ₑ is the number of free electrons,
• 𝑁ᵢ ₋ ₁ is the number of neutral atoms,
• 𝑚ₑ​ is the electron mass,
• 𝑘 is the Boltzmann constant,
• 𝑇 is the temperature,
• ℎ is the Planck constant,
• 𝑍ᵢ​ is the partition function for the ionized state,
• 𝑍ᵢ ₋ ₁​ is the partition function for the neutral state,
• 𝐸ᵢ​ is the ionization energy from state 𝑖−1 to state i,
• 𝑒 is the base of natural logarithms.

This equation models the ionization balance in astrophysical plasmas and helps in determining the physical conditions of stellar atmospheres.

Saha Ionization Equation Derivation

Understanding the Basic Concept

The Saha Ionization Equation is derived by considering how atoms in a gas can exist in different states—either as neutral atoms or as ionized atoms (atoms missing one or more electrons). The transition between these states involves either the absorption or release of energy, specifically the energy required to remove an electron from an atom.

Applying Thermodynamics

To derive the equation, we start by applying the principles of thermodynamics and statistical mechanics. These principles tell us that the behavior of atoms and electrons in a gas at a given temperature and pressure can be predicted by understanding the distribution of energy among them.

Considering Equilibrium

In a state of thermal equilibrium, the arrangement of electrons and ions in a gas reaches a balance. This balance isn’t static; electrons are continually being knocked out of atoms (ionizing them) and re-captured (re-forming neutral atoms), but the rate of ionization and the rate of recombination are equal, so the overall system remains in equilibrium.

Relating to Energy Levels

The likelihood of an atom being ionized or remaining neutral depends on the energy available to it (from the environment, such as thermal energy at a given temperature) and the energy required to ionize the atom. The higher the temperature, the more thermal energy is available, increasing the likelihood of ionization.

Statistical Considerations

Statistical mechanics provides a framework to calculate the relative populations of neutral and ionized atoms based on their energy states and the temperature of the surrounding environment. It considers all possible energy states of atoms and the statistical likelihood of each state being occupied.

Equating Conditions

The final step in deriving the equation involves setting up an equality condition where the rate at which atoms are ionized equals the rate at which ions recombine into neutral atoms. This involves considering the density of neutral atoms, the density of ions, and the density of free electrons, along with how these quantities change with temperature.

Uses of Saha Ionization Equation

• Astrophysics: It helps determine the ionization states of elements in stellar atmospheres, crucial for understanding star temperatures and luminosities.
• Plasma Physics: The equation is used to analyze the ionization equilibrium in laboratory plasmas, important for fusion research and industrial applications.
• Spectroscopy: It assists in interpreting spectral lines from hot gases, aiding in the identification of elements and their states in various environments.
• Material Science: The equation is employed to study ionized gases used in the manufacturing of semiconductors and other materials.
• Cosmology: It plays a role in understanding the ionization history of the early universe, particularly during the reionization epoch.
• Astrochemistry: The equation aids in exploring the chemical composition and reactions within interstellar clouds where stars form, impacting the study of molecular clouds and star formation.

Examples for Saha Ionization Equation

1. Stellar Atmospheres: Astronomers use the Saha Ionization Equation to determine the temperature of stars. By analyzing the ionization levels of different elements in a star’s atmosphere, they can infer the star’s surface temperature and luminosity.
2. Spectroscopic Analysis: In laboratories, spectroscopists apply the Saha Ionization Equation to interpret the spectral lines of elements heated to high temperatures. This helps in identifying elements and their ionization states, crucial for materials science and chemical analysis.
3. Plasma Diagnostics: Plasma physicists use the equation to understand the properties of plasma in both natural settings (like the solar corona) and in controlled environments (such as fusion reactors). The ionization states calculated help in modeling plasma behavior and optimizing reactor conditions.
4. Understanding Early Universe Chemistry: Cosmologists apply the Saha Ionization Equation to model the ionization processes occurring in the early universe, particularly during the recombination era. This is key to understanding the formation of the cosmic microwave background radiation.
5. Planetary Atmospheres: The equation is used in planetary science to model the ionization of gases in the atmospheres of planets and moons. This helps in predicting atmospheric composition, weather patterns, and potential for electrical phenomena like auroras.

FAQ’S

What is the importance of the Saha equation?

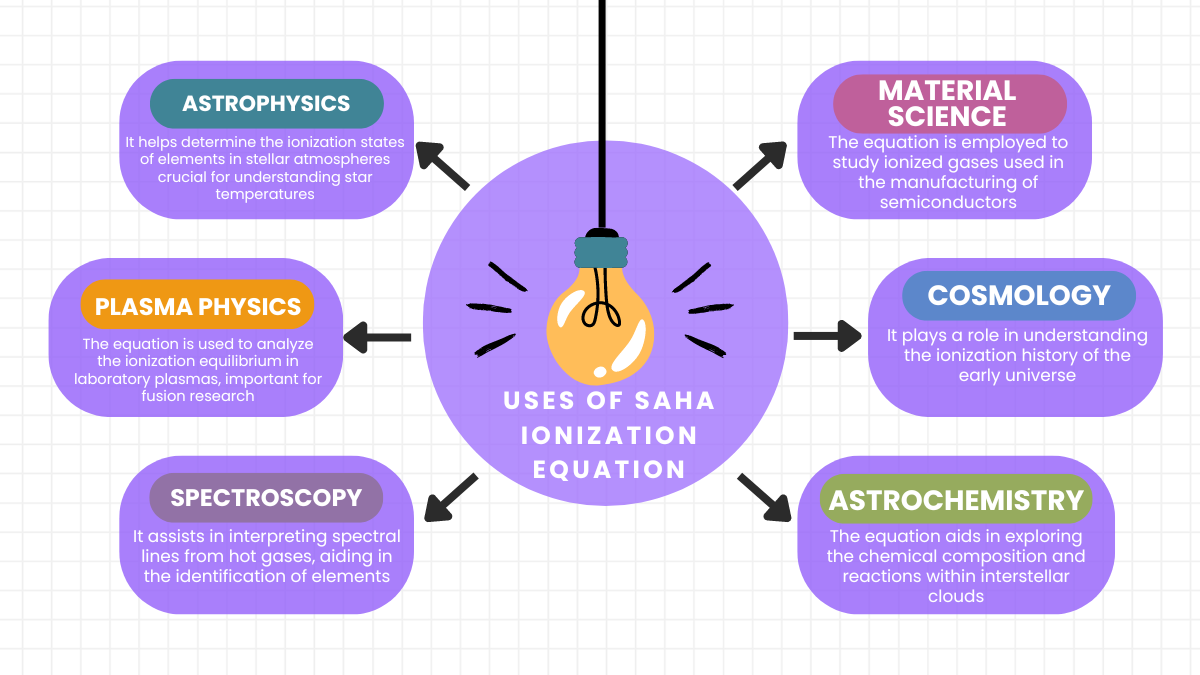
The Saha equation is crucial for determining ionization states in plasmas, essential in astrophysics for analyzing stellar atmospheres and understanding cosmic phenomena.

What is the Saha Boltzmann method?

The Saha-Boltzmann method combines the Saha Ionization Equation and Boltzmann distribution to analyze the thermal and ionization equilibrium in stellar atmospheres, thereby decoding star compositions and temperatures.

At what temperature is hydrogen ionized?

Hydrogen begins to ionize at about 10,000 Kelvin, a temperature where enough energy is available to start stripping electrons from hydrogen atoms, significantly seen in stars.