Factors are numbers that divide another number exactly without leaving a remainder. Learning factors from 1 to 100 strengthens arithmetic and problem-solving skills. Factors are essential concepts in mathematics, algebra, and number theory.
Download Factors of 1 to 100 in PDF
Factors of 1 to 100
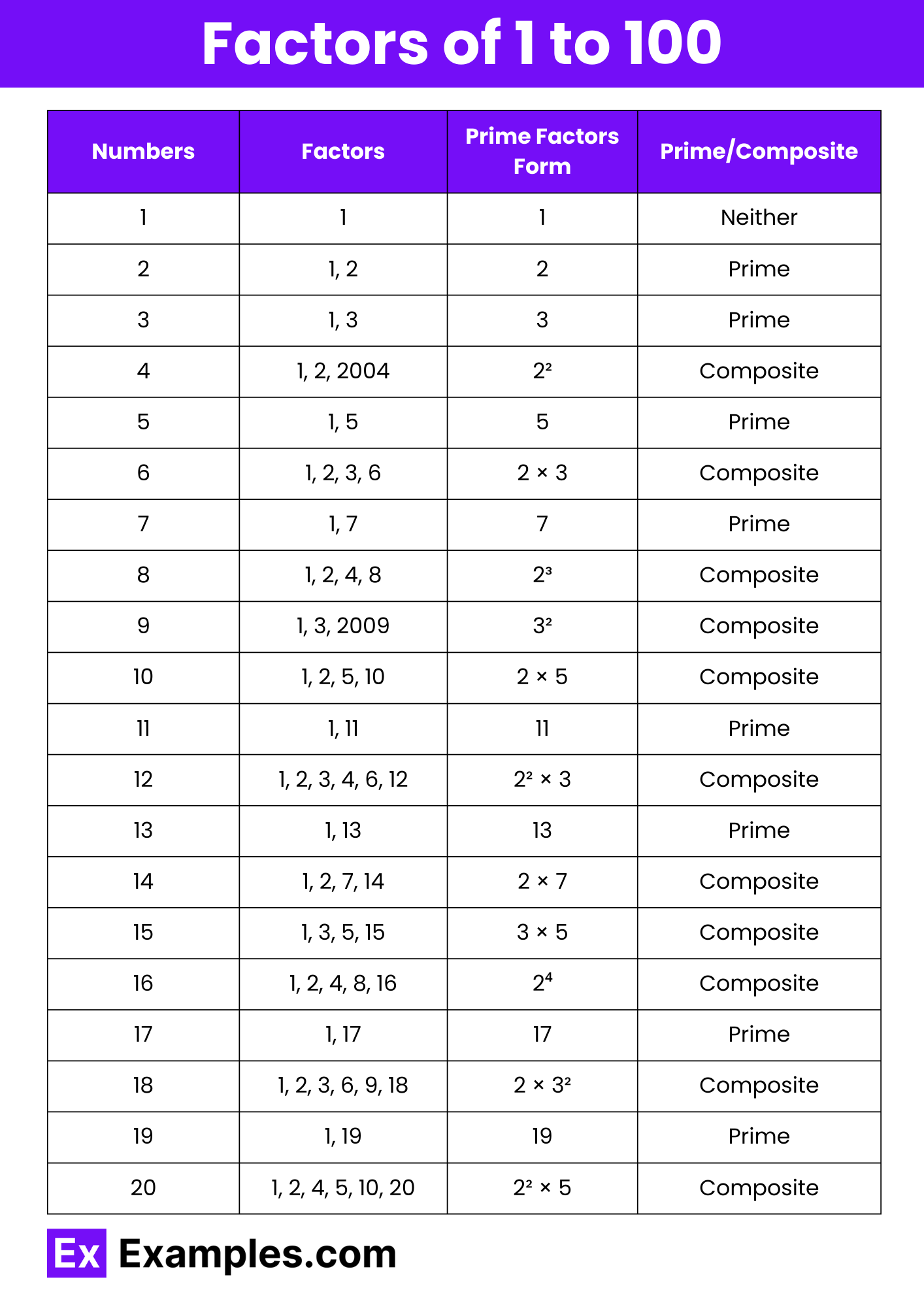
Download Factors of 1 to 100 in PDF
| Numbers | Factors | Prime Factors Form | Prime/Composite |
|---|---|---|---|
| 1 | 1 | 1 | Neither |
| 2 | 1, 2 | 2 | Prime |
| 3 | 1, 3 | 3 | Prime |
| 4 | 1, 2, 4 | 2² | Composite |
| 5 | 1, 5 | 5 | Prime |
| 6 | 1, 2, 3, 6 | 2 × 3 | Composite |
| 7 | 1, 7 | 7 | Prime |
| 8 | 1, 2, 4, 8 | 2³ | Composite |
| 9 | 1, 3, 9 | 3² | Composite |
| 10 | 1, 2, 5, 10 | 2 × 5 | Composite |
| 11 | 1, 11 | 11 | Prime |
| 12 | 1, 2, 3, 4, 6, 12 | 2² × 3 | Composite |
| 13 | 1, 13 | 13 | Prime |
| 14 | 1, 2, 7, 14 | 2 × 7 | Composite |
| 15 | 1, 3, 5, 15 | 3 × 5 | Composite |
| 16 | 1, 2, 4, 8, 16 | 2⁴ | Composite |
| 17 | 1, 17 | 17 | Prime |
| 18 | 1, 2, 3, 6, 9, 18 | 2 × 3² | Composite |
| 19 | 1, 19 | 19 | Prime |
| 20 | 1, 2, 4, 5, 10, 20 | 2² × 5 | Composite |
| 21 | 1, 3, 7, 21 | 3 × 7 | Composite |
| 22 | 1, 2, 11, 22 | 2 × 11 | Composite |
| 23 | 1, 23 | 23 | Prime |
| 24 | 1, 2, 3, 4, 6, 8, 12, 24 | 2³ × 3 | Composite |
| 25 | 1, 5, 25 | 5² | Composite |
| 26 | 1, 2, 13, 26 | 2 × 13 | Composite |
| 27 | 1, 3, 9, 27 | 3³ | Composite |
| 28 | 1, 2, 4, 7, 14, 28 | 2² × 7 | Composite |
| 29 | 1, 29 | 29 | Prime |
| 30 | 1, 2, 3, 5, 6, 10, 15, 30 | 2 × 3 × 5 | Composite |
| 31 | 1, 31 | 31 | Prime |
| 32 | 1, 2, 4, 8, 16, 32 | 2⁵ | Composite |
| 33 | 1, 3, 11, 33 | 3 × 11 | Composite |
| 34 | 1, 2, 17, 34 | 2 × 17 | Composite |
| 35 | 1, 5, 7, 35 | 5 × 7 | Composite |
| 36 | 1, 2, 3, 4, 6, 9, 12, 18, 36 | 2² × 3² | Composite |
| 37 | 1, 37 | 37 | Prime |
| 38 | 1, 2, 19, 38 | 2 × 19 | Composite |
| 39 | 1, 3, 13, 39 | 3 × 13 | Composite |
| 40 | 1, 2, 4, 5, 8, 10, 20, 40 | 2³ × 5 | Composite |
| 41 | 1, 41 | 41 | Prime |
| 42 | 1, 2, 3, 6, 7, 14, 21, 42 | 2 × 3 × 7 | Composite |
| 43 | 1, 43 | 43 | Prime |
| 44 | 1, 2, 4, 11, 22, 44 | 2² × 11 | Composite |
| 45 | 1, 3, 5, 9, 15, 45 | 3² × 5 | Composite |
| 46 | 1, 2, 23, 46 | 2 × 23 | Composite |
| 47 | 1, 47 | 47 | Prime |
| 48 | 1, 2, 3, 4, 6, 8, 12, 16, 24, 48 | 2⁴ × 3 | Composite |
| 49 | 1, 7, 49 | 7² | Composite |
| 50 | 1, 2, 5, 10, 25, 50 | 2 × 5² | Composite |
| 51 | 1, 3, 17, 51 | 3 × 17 | Composite |
| 52 | 1, 2, 4, 13, 26, 52 | 2² × 13 | Composite |
| 53 | 1, 53 | 53 | Prime |
| 54 | 1, 2, 3, 6, 9, 18, 27, 54 | 2 × 3³ | Composite |
| 55 | 1, 5, 11, 55 | 5 × 11 | Composite |
| 56 | 1, 2, 4, 7, 8, 14, 28, 56 | 2³ × 7 | Composite |
| 57 | 1, 3, 19, 57 | 3 × 19 | Composite |
| 58 | 1, 2, 29, 58 | 2 × 29 | Composite |
| 59 | 1, 59 | 59 | Prime |
| 60 | 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 | 2² × 3 × 5 | Composite |
| 61 | 1, 61 | 61 | Prime |
| 62 | 1, 2, 31, 62 | 2 × 31 | Composite |
| 63 | 1, 3, 7, 9, 21, 63 | 3² × 7 | Composite |
| 64 | 1, 2, 4, 8, 16, 32, 64 | 2⁶ | Composite |
| 65 | 1, 5, 13, 65 | 5 × 13 | Composite |
| 66 | 1, 2, 3, 6, 11, 22, 33, 66 | 2 × 3 × 11 | Composite |
| 67 | 1, 67 | 67 | Prime |
| 68 | 1, 2, 4, 17, 34, 68 | 2² × 17 | Composite |
| 69 | 1, 3, 23, 69 | 3 × 23 | Composite |
| 70 | 1, 2, 5, 7, 10, 14, 35, 70 | 2 × 5 × 7 | Composite |
| 71 | 1, 71 | 71 | Prime |
| 72 | 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72 | 2³ × 3² | Composite |
| 73 | 1, 73 | 73 | Prime |
| 74 | 1, 2, 37, 74 | 2 × 37 | Composite |
| 75 | 1, 3, 5, 15, 25, 75 | 3 × 5² | Composite |
| 76 | 1, 2, 4, 19, 38, 76 | 2² × 19 | Composite |
| 77 | 1, 7, 11, 77 | 7 × 11 | Composite |
| 78 | 1, 2, 3, 6, 13, 26, 39, 78 | 2 × 3 × 13 | Composite |
| 79 | 1, 79 | 79 | Prime |
| 80 | 1, 2, 4, 5, 8, 10, 16, 20, 40, 80 | 2⁴ × 5 | Composite |
| 81 | 1, 3, 9, 27, 81 | 3⁴ | Composite |
| 82 | 1, 2, 41, 82 | 2 × 41 | Composite |
| 83 | 1, 83 | 83 | Prime |
| 84 | 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84 | 2² × 3 × 7 | Composite |
| 85 | 1, 5, 17, 85 | 5 × 17 | Composite |
| 86 | 1, 2, 43, 86 | 2 × 43 | Composite |
| 87 | 1, 3, 29, 87 | 3 × 29 | Composite |
| 88 | 1, 2, 4, 8, 11, 22, 44, 88 | 2³ × 11 | Composite |
| 89 | 1, 89 | 89 | Prime |
| 90 | 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90 | 2 × 3² × 5 | Composite |
| 91 | 1, 7, 13, 91 | 7 × 13 | Composite |
| 92 | 1, 2, 4, 23, 46, 92 | 2² × 23 | Composite |
| 93 | 1, 3, 31, 93 | 3 × 31 | Composite |
| 94 | 1, 2, 47, 94 | 2 × 47 | Composite |
| 95 | 1, 5, 19, 95 | 5 × 19 | Composite |
| 96 | 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96 | 2⁵ × 3 | Composite |
| 97 | 1, 97 | 97 | Prime |
| 98 | 1, 2, 7, 14, 49, 98 | 2 × 7² | Composite |
| 99 | 1, 3, 9, 11, 33, 99 | 3² × 11 | Composite |
| 100 | 1, 2, 4, 5, 10, 20, 25, 50, 100 | 2² × 5² | Composite |
The factors of numbers from 1 to 100 reveal the unique divisibility properties of each number, highlighting their primes and composites. Factors range from 1, which only has itself as a factor, to 100, which has multiple pairs of factors such as 1 and 100, 2 and 50, 4 and 25, and so forth. This study of factors illustrates the fundamental arithmetic relationships and patterns, such as even numbers always having 2 as a factor and primes only having 1 and themselves as factors. Understanding these factors is crucial for simplifying fractions, finding greatest common divisors, and solving various mathematical problems efficiently.