Which of the following is a factor of 504?
7
15
20
25

Factors are the numbers that divide a given number exactly without leaving a remainder. Identifying the factors of numbers helps in various mathematical operations, such as simplifying fractions, finding greatest common divisors (GCD), and least common multiples (LCM). Understanding the factors of a number is crucial in number theory and algebra.
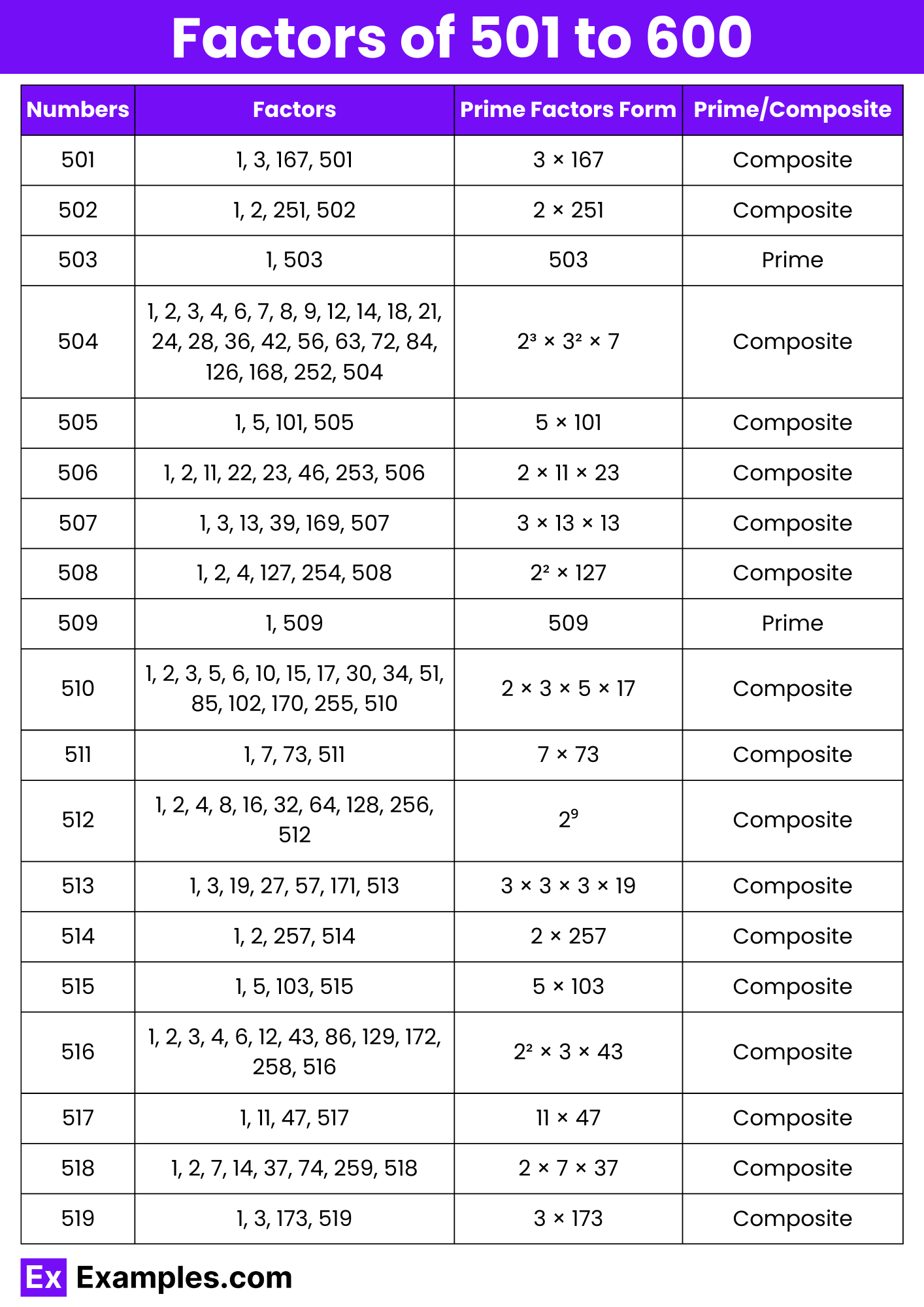
In this guide, we will explore the factors of numbers from 501 to 600. For each number, we will list all its factors and determine its prime factorization, which breaks down the number into its basic prime components. This examination provides insights into the structure and properties of numbers, facilitating a deeper comprehension of mathematical principles. Let’s delve into the factors and prime factorizations of numbers from 501 to 600.
Download Factors of 501 to 600 in PDF
Download Factors of 501 to 600 in PDF
| Numbers | Factors | Prime Factors Form | Prime/Composite |
|---|---|---|---|
| 501 | 1, 3, 167, 501 | 3 × 167 | Composite |
| 502 | 1, 2, 251, 502 | 2 × 251 | Composite |
| 503 | 1, 503 | 503 | Prime |
| 504 | 1, 2, 3, 4, 6, 7, 8, 9, 12, 14, 18, 21, 24, 28, 36, 42, 56, 63, 72, 84, 126, 168, 252, 504 | 2³ × 3² × 7 | Composite |
| 505 | 1, 5, 101, 505 | 5 × 101 | Composite |
| 506 | 1, 2, 11, 22, 23, 46, 253, 506 | 2 × 11 × 23 | Composite |
| 507 | 1, 3, 13, 39, 169, 507 | 3 × 13 × 13 | Composite |
| 508 | 1, 2, 4, 127, 254, 508 | 2² × 127 | Composite |
| 509 | 1, 509 | 509 | Prime |
| 510 | 1, 2, 3, 5, 6, 10, 15, 17, 30, 34, 51, 85, 102, 170, 255, 510 | 2 × 3 × 5 × 17 | Composite |
| 511 | 1, 7, 73, 511 | 7 × 73 | Composite |
| 512 | 1, 2, 4, 8, 16, 32, 64, 128, 256, 512 | 2⁹ | Composite |
| 513 | 1, 3, 19, 27, 57, 171, 513 | 3 × 3 × 3 × 19 | Composite |
| 514 | 1, 2, 257, 514 | 2 × 257 | Composite |
| 515 | 1, 5, 103, 515 | 5 × 103 | Composite |
| 516 | 1, 2, 3, 4, 6, 12, 43, 86, 129, 172, 258, 516 | 2² × 3 × 43 | Composite |
| 517 | 1, 11, 47, 517 | 11 × 47 | Composite |
| 518 | 1, 2, 7, 14, 37, 74, 259, 518 | 2 × 7 × 37 | Composite |
| 519 | 1, 3, 173, 519 | 3 × 173 | Composite |
| 520 | 1, 2, 4, 5, 8, 10, 13, 20, 26, 40, 52, 65, 104, 130, 260, 520 | 2³ × 5 × 13 | Composite |
| 521 | 1, 521 | 521 | Prime |
| 522 | 1, 2, 3, 6, 9, 18, 29, 58, 87, 174, 261, 522 | 2 × 3 × 3 × 29 | Composite |
| 523 | 1, 523 | 523 | Prime |
| 524 | 1, 2, 4, 131, 262, 524 | 2² × 131 | Composite |
| 525 | 1, 3, 5, 7, 15, 21, 25, 35, 75, 105, 175, 525 | 3 × 5² × 7 | Composite |
| 526 | 1, 2, 263, 526 | 2 × 263 | Composite |
| 527 | 1, 17, 31, 527 | 17 × 31 | Composite |
| 528 | 1, 2, 3, 4, 6, 8, 12, 16, 22, 24, 33, 44, 66, 88, 132, 176, 264, 528 | 2⁴ × 3 × 11 | Composite |
| 529 | 1, 23, 529 | 23² | Composite |
| 530 | 1, 2, 5, 10, 53, 106, 265, 530 | 2 × 5 × 53 | Composite |
| 531 | 1, 3, 9, 59, 177, 531 | 3 × 3 × 59 | Composite |
| 532 | 1, 2, 4, 7, 14, 19, 28, 38, 76, 133, 266, 532 | 2² × 7 × 19 | Composite |
| 533 | 1, 13, 41, 533 | 13 × 41 | Composite |
| 534 | 1, 2, 3, 6, 89, 178, 267, 534 | 2 × 3 × 89 | Composite |
| 535 | 1, 5, 107, 535 | 5 × 107 | Composite |
| 536 | 1, 2, 4, 8, 67, 134, 268, 536 | 2³ × 67 | Composite |
| 537 | 1, 3, 179, 537 | 3 × 179 | Composite |
| 538 | 1, 2, 269, 538 | 2 × 269 | Composite |
| 539 | 1, 7, 11, 49, 77, 539 | 7 × 11² | Composite |
| 540 | 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 27, 30, 36, 45, 54, 60, 90, 108, 135, 180, 270, 540 | 2² × 3³ × 5 | Composite |
| 541 | 1, 541 | 541 | Prime |
| 542 | 1, 2, 271, 542 | 2 × 271 | Composite |
| 543 | 1, 3, 181, 543 | 3 × 181 | Composite |
| 544 | 1, 2, 4, 8, 16, 32, 68, 136, 272, 544 | 2⁵ × 17 | Composite |
| 545 | 1, 5, 109, 545 | 5 × 109 | Composite |
| 546 | 1, 2, 3, 6, 7, 13, 14, 21, 26, 39, 42, 78, 91, 182, 273, 546 | 2 × 3 × 7 × 13 | Composite |
| 547 | 1, 547 | 547 | Prime |
| 548 | 1, 2, 4, 137, 274, 548 | 2² × 137 | Composite |
| 549 | 1, 3, 9, 61, 183, 549 | 3² × 61 | Composite |
| 550 | 1, 2, 5, 10, 11, 22, 25, 50, 55, 110, 275, 550 | 2 × 5² × 11 | Composite |
| 551 | 1, 19, 29, 551 | 19 × 29 | Composite |
| 552 | 1, 2, 3, 4, 6, 8, 12, 23, 24, 46, 69, 92, 138, 184, 276, 552 | 2³ × 3 × 23 | Composite |
| 553 | 1, 7, 79, 553 | 7 × 79 | Composite |
| 554 | 1, 2, 277, 554 | 2 × 277 | Composite |
| 555 | 1, 3, 5, 15, 37, 111, 185, 555 | 3 × 5 × 37 | Composite |
| 556 | 1, 2, 4, 139, 278, 556 | 2² × 139 | Composite |
| 557 | 1, 557 | 557 | Prime |
| 558 | 1, 2, 3, 6, 31, 62, 93, 186, 279, 558 | 2 × 3 × 31 | Composite |
| 559 | 1, 13, 43, 559 | 13 × 43 | Composite |
| 560 | 1, 2, 4, 5, 7, 8, 10, 14, 16, 20, 28, 35, 40, 56, 70, 80, 112, 140, 280, 560 | 2⁴ × 5 × 7 | Composite |
| 561 | 1, 3, 11, 17, 33, 51, 187, 561 | 3 × 11 × 17 | Composite |
| 562 | 1, 2, 281, 562 | 2 × 281 | Composite |
| 563 | 1, 563 | 563 | Prime |
| 564 | 1, 2, 3, 4, 6, 12, 47, 94, 141, 188, 282, 564 | 2² × 3 × 47 | Composite |
| 565 | 1, 5, 113, 565 | 5 × 113 | Composite |
| 566 | 1, 2, 283, 566 | 2 × 283 | Composite |
| 567 | 1, 3, 7, 9, 21, 27, 63, 81, 189, 567 | 3⁴ × 7 | Composite |
| 568 | 1, 2, 4, 8, 71, 142, 284, 568 | 2³ × 71 | Composite |
| 569 | 1, 569 | 569 | Prime |
| 570 | 1, 2, 3, 5, 6, 10, 15, 19, 30, 38, 57, 95, 114, 190, 285, 570 | 2 × 3 × 5 × 19 | Composite |
| 571 | 1, 571 | 571 | Prime |
| 572 | 1, 2, 4, 11, 22, 26, 44, 52, 143, 286, 572 | 2² × 11 × 13 | Composite |
| 573 | 1, 3, 191, 573 | 3 × 191 | Composite |
| 574 | 1, 2, 7, 14, 41, 82, 287, 574 | 2 × 7 × 41 | Composite |
| 575 | 1, 5, 23, 25, 115, 575 | 5² × 23 | Composite |
| 576 | 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 64, 72, 96, 144, 192, 288, 576 | 2⁶ × 3² | Composite |
| 577 | 1, 577 | 577 | Prime |
| 578 | 1, 2, 17, 34, 289, 578 | 2 × 17² | Composite |
| 579 | 1, 3, 193, 579 | 3 × 193 | Composite |
| 580 | 1, 2, 4, 5, 10, 20, 29, 58, 116, 145, 290, 580 | 2² × 5 × 29 | Composite |
| 581 | 1, 7, 83, 581 | 7 × 83 | Composite |
| 582 | 1, 2, 3, 6, 97, 194, 291, 582 | 2 × 3 × 97 | Composite |
| 583 | 1, 11, 53, 583 | 11 × 53 | Composite |
| 584 | 1, 2, 4, 8, 73, 146, 292, 584 | 2³ × 73 | Composite |
| 585 | 1, 3, 5, 9, 13, 15, 27, 39, 45, 65, 117, 195, 585 | 3 × 5 × 3² | Composite |
| 586 | 1, 2, 293, 586 | 2 × 293 | Composite |
| 587 | 1, 587 | 587 | Prime |
| 588 | 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 49, 84, 98, 147, 196, 294, 588 | 2² × 3 × 7² | Composite |
| 589 | 1, 19, 31, 589 | 19 × 31 | Composite |
| 590 | 1, 2, 5, 10, 59, 118, 295, 590 | 2 × 5 × 59 | Composite |
| 591 | 1, 3, 197, 591 | 3 × 197 | Composite |
| 592 | 1, 2, 4, 8, 16, 37, 74, 148, 296, 592 | 2⁴ × 37 | Composite |
| 593 | 1, 593 | 593 | Prime |
| 594 | 1, 2, 3, 6, 9, 18, 33, 54, 99, 198, 297, 594 | 2 × 3³ × 11 | Composite |
| 595 | 1, 5, 7, 17, 35, 85, 119, 595 | 5 × 7 × 17 | Composite |
| 596 | 1, 2, 4, 149, 298, 596 | 2² × 149 | Composite |
| 597 | 1, 3, 199, 597 | 3 × 199 | Composite |
| 598 | 1, 2, 13, 23, 26, 46, 299, 598 | 2 × 13 × 23 | Composite |
| 599 | 1, 599 | 599 | Prime |
| 600 | 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 25, 30, 40, 50, 60, 75, 100, 120, 150, 200, 300, 600 | 2³ × 3 × 5² | Composite |
The factors of numbers from 501 to 600 demonstrate the variety and complexity of divisors within this range. Each number has its unique set of factors, which include prime numbers and their multiples. Understanding these factors is crucial for various mathematical applications such as simplifying fractions, finding greatest common divisors, and solving problems involving multiples. For instance, 501 has factors 1, 3, 167, and 501, while 600 has a more extensive set including 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 25, 30, 40, 50, 60, 75, 100, 120, 150, 200, 300, and 600. This range emphasizes the importance of factorization in number theory and its practical applications in both elementary and advanced mathematics.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
Which of the following is a factor of 504?
7
15
20
25
What are the factors of 525?
1, 3, 5, 7, 15, 21, 25, 35, 75, 105, 175, 525
1, 3, 5, 15, 25, 35, 75, 105, 175
1, 5, 21, 25, 105, 525
1, 5, 7, 25, 35, 75, 525
Which number has factors 1, 8, 16, 32, and 64?
64
128
256
512
What is the greatest common divisor (GCD) of 540 and 630?
30
60
90
120
Which of the following is not a factor of 555?
15
30
50
75
What are the factors of 576?
1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 27, 32, 36, 48, 54, 72, 96, 144, 192, 288, 576
1, 2, 4, 6, 8, 12, 16, 18, 24, 36, 48, 72, 96, 144, 192, 576
1, 2, 4, 8, 12, 18, 24, 36, 48, 72, 144, 576
1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 576
Which number is a factor of both 510 and 552?
10
12
15
20
What are the factors of 585?
1, 5, 9, 13, 39, 195, 585
1, 3, 5, 9, 13, 15, 39, 65, 117, 195, 585
1, 3, 5, 13, 39, 65, 117, 585
1, 3, 9, 13, 39, 117, 585
Which number is a factor of 594?
4
7
9
15
Which of the following is not a factor of 525?
7
21
30
40
Before you leave, take our quick quiz to enhance your learning!

